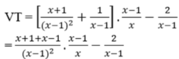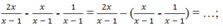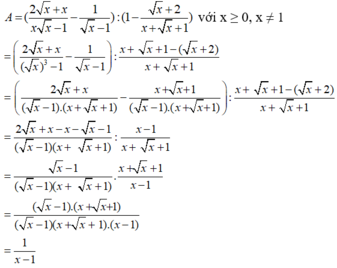1+1+1+1+1+1+1+1+1+1+1+1+1x 0 +1

Những câu hỏi liên quan
Chứng minh rằng:
x
+
1
x
-
2
x
+
1
+
1
x
-
1
:
x
x
-
1
-...
Đọc tiếp
Chứng minh rằng:
x + 1 x - 2 x + 1 + 1 x - 1 : x x - 1 - 2 x - 1 = 0
1+1+1+1+1+1+1+1+1x 0+1+2=?
Kết quả phép tính trên là:
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 x 0 + 1 + 2 = 11
Đáp số: 11
Các bạn nên nhớ là nhân chia trước, cộng trừ sau.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
G = (x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)(x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)
a) Rút gọn G b) Tìm giá trị nhỏ nhất của G với x > 0
c) Tính G tại | x - 3 | = 2 d) Tìm x với G = 1 ; G < 0
Thực hiện phép trừ
2
x
x
-
1
-
x
x
-
1
-
1
x
-
1
. Cách thực hiện nào sau đây là sai ?A.
2
x
x
-...
Đọc tiếp
Thực hiện phép trừ 2 x x - 1 - x x - 1 - 1 x - 1 . Cách thực hiện nào sau đây là sai ?
A. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - x x - 1 - 1 x - 1 = . . .
B. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - x x - 1 - 1 x - 1 = . . .
C. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - x x - 1 + 1 x - 1 = . . .
D. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - - x x - 1 + - 1 x - 1 = . . .
1+1+1+1+1+1+1+1+1+1+1+1+1+1+1x(0+0) =?
Ai nhanh nhất thì mk k và gửi lời mời kb vs mk nhé!!!!! Arigatou gozaimasuta!!!!
Xem thêm câu trả lời
Cho
x
0
,
y
0
,
z
0
x
y
z
1
. Chứng minh rằng
1
x...
Đọc tiếp
Cho x > 0 , y > 0 , z > 0 x y z = 1 . Chứng minh rằng 1 x + y + 1 + 1 y + z + 1 + 1 z + x + 1 ≤ 1
Đ ặ t x = a 3 y = b 3 z = c 3 , v ì x , y , z > 0 x y z = 1 = > a , b , c > 0 a b c = 1
Ta có: x + y + 1 = a 3 + b 3 + 1 = ( a + b ) ( a 2 − a b + b 2 ) + 1 ≥ ( a + b ) a b + 1 = a b ( a + b + c ) = a + b + c c
Do đó: 1 x + y + 1 ≤ c a + b + c
Tương tự ta có: 1 y + z + 1 ≤ a a + b + c 1 z + x + 1 ≤ b a + b + c
Cộng 3 bất đẳng thức trên theo vế ta có đpcm
Đúng 0
Bình luận (0)
Phương trình 1 x - 1 + 1 x + 1 + 1 x - 4 = 0 có số nghiệm là:
A. 1
B. 0
C. 2
D. 3
Rút gọn biểu thức:
A
2
x
+
x
x
x
−
1
−
1
x
−
1
:
1
−...
Đọc tiếp
Rút gọn biểu thức: A = 2 x + x x x − 1 − 1 x − 1 : 1 − x + 2 x + x + 1 với x ≥ 0, x ≠ 1
A. 1 x - 1
B. x x - 1
C. x-1
D. x - 1 x