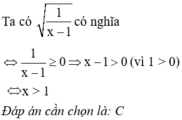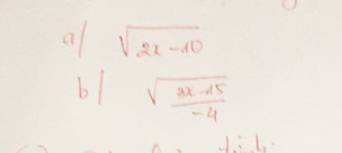
Tìm điều kiện có nghĩa cho căn thức

Những câu hỏi liên quan
tìm điều kiện để căn thức sau có nghĩa
a)√25x
Tìm điều kiện của x để căn thức 1 x - 1 có nghĩa.
A. x ≥ 1
B. x < 1
C. x > 1
D. x = 1
tìm điều kiện của x để căn thức sau có nghĩa
căn 2020 + căn -3 phần x+3
\(\sqrt{2020}+\sqrt{-\frac{3}{x+3}}\)
Căn thức trên có nghĩa khi:\(\hept{\begin{cases}x+3\ne0\\-\frac{3}{x+3}>0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ne-3\\x+3< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ne-3\\x< -3\end{cases}}}}\)
\(\Rightarrow x< -3\)
tìm điều kiện để căn thức có nghĩa:\(\sqrt{4x-x^2-2}\)
\(\sqrt{4x-x^2-2}\)
ĐKXĐ : \(4x-x^2-2\ge0\)
\(\Leftrightarrow x^2-4x+2\le0\)
Ta có : \(x^2-4x+2=0\)
\(\Delta=b^2-4ac=\left(-4\right)^2-4\cdot1\cdot2=8>0\)
=> Phương trình có hai nghiệm
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{4-\sqrt{8}}{2}=2-\sqrt{2}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{4+\sqrt{8}}{2}=2+\sqrt{2}\)
Để \(x^2-4x+2\le0\)
\(\Rightarrow\orbr{\begin{cases}x\ge2+\sqrt{2}\\x\le2-\sqrt{2}\end{cases}}\)
Vậy ....
Đúng 0
Bình luận (0)
tìm điều kiện xác định để biểu thức sau có nghĩa căn của cả x+3/7-x
\(\sqrt{x+\frac{3}{7-x}}hay\sqrt{x+\frac{3}{7}-x}\) vậy?
Đúng 0
Bình luận (0)
Để \(\sqrt{\frac{x+3}{7-x}}\)có nghĩa thì x + 3 và 7 - x cùng dấu
\(TH1:\hept{\begin{cases}x+3\ge0\\7-x>0\end{cases}}\Rightarrow\hept{\begin{cases}x\ge-3\\x< 7\end{cases}}\Rightarrow-3\le x< 7\)(Vì x = 7 thì bt không có nghĩa)
\(TH2:\hept{\begin{cases}x+3\le0\\7-x< 0\end{cases}}\Rightarrow\hept{\begin{cases}x\le-3\\x>7\end{cases}}\left(L\right)\)
Vậy \(-3\le x< 7\)
Tìm điều kiện để căn thức có nghĩa :
\(\sqrt{x^2-5}\)
\(\sqrt{x^2-5}\ge0\Rightarrow x^2-5\ge0\)
\(\Rightarrow x^2\ge5\)
\(\Rightarrow x\ge\sqrt{5}\)
Đúng 0
Bình luận (0)
Vy Thị Hoàng Lan\(=-\sqrt{5}\)vẫn đúng nhé.
Ta có: \(\sqrt{x^2-5}=\sqrt{\left(x+\sqrt{5}\right)\left(x-\sqrt{5}\right)}\)
Để căn thức có nghĩa thì \(x+\sqrt{5}\)và \(x-\sqrt{5}\)cùng dấu
\(TH1:\hept{\begin{cases}x+\sqrt{5}\ge0\\x-\sqrt{5}\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge-\sqrt{5}\\x\ge\sqrt{5}\end{cases}}\Leftrightarrow x\ge\sqrt{5}\)
\(TH1:\hept{\begin{cases}x+\sqrt{5}\le0\\x-\sqrt{5}\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le-\sqrt{5}\\x\le\sqrt{5}\end{cases}}\Leftrightarrow x\le-\sqrt{5}\)
Đúng 0
Bình luận (0)
bác pro nào k sai thì chỉ chỗ giùm
Đúng 0
Bình luận (0)
TÌM x
A) căn (25x)^2=/-3/^2
Tìm điều kiện để các căn thức có nghĩa
A) căn (-3/x+2)
B)căn (-3/1+x^2)
tìm điều kiện để căn thức có nghĩa:
\(\sqrt{12x^2-17x-5}\)
Sửa đề lại cho đúng nhé :
\(\sqrt{12x^2-17x+5}=\sqrt{12x^2-12x-5x+5}\)
\(=\)\(\sqrt{12x\left(x-1\right)-5\left(x-1\right)}=\sqrt{\left(x-1\right)\left(12x-5\right)}\)
\(btxđ\Leftrightarrow\left(x-1\right)\left(12x-5\right)\ge0\)
\(\Rightarrow\orbr{\begin{cases}x-1\ge0;12x-5\ge0\\x-1< 0;12x-5< 0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x\ge1;x\le\frac{12}{5}\left(tm\right)\\x< 1;x>\frac{12}{5}\left(ktm\right)\end{cases}}\)
\(\Rightarrow1\le x\le\frac{12}{5}\)
Đúng 0
Bình luận (0)
hình như ko phải \(\frac{12}{5}\)mà là \(\frac{5}{12}\)
Đúng 0
Bình luận (0)
Rất xin lỗi nha , cho sửa lại chút :
\(\Rightarrow\orbr{\begin{cases}x-1\ge0;12x-5\ge0\\x-1< 0;12x-5< 0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x\ge1;x\ge\frac{5}{12}\\x< 1;x< \frac{5}{12}\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x\ge1\\x< \frac{5}{12}\end{cases}}\)
Vậy \(x\ge1\)Hoặc \(x< \frac{5}{12}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
\(\frac{\sqrt{-3x}}{x^2-1}\) Tìm điều kiện để căn thức có nghĩa
\(\frac{\sqrt{-3x}}{x^2-1}\)
Điều kiện để căn thức có nghĩa là :
\(\hept{\begin{cases}x^2-1\ne0\\-3x\ge0\end{cases}}< =>\hept{\begin{cases}x\ne\pm1\\x\le0\end{cases}}\)
Tìm điều kiện để căn thức sau có nghĩa
\(\sqrt{-x^2-1}\)