X2 + 16X+ 64
16X2 - 8X +4
25X2+ 10X +1
X2 - 12X + 36
4X2- 4X + 1
X2 - 2X+ 1
X2 + X+ 1/4
Những câu hỏi liên quan
Tổng các nghiệm của phương trình:
1
x
2
+
4
x
+
3
+
1
x
2
+
8
x
+
15
+
1
x...
Đọc tiếp
Tổng các nghiệm của phương trình: 1 x 2 + 4 x + 3 + 1 x 2 + 8 x + 15 + 1 x 2 + 12 x + 35 + 1 x 2 + 16 x + 63 = 1 5 là
A. 10
B. -10
C. -11
D. 12
Biết
x
0
là nghiệm nhỏ nhất của phương trình
1
x
2
+
4
x
+
3
+
1
x
2
+
8
x...
Đọc tiếp
Biết x 0 là nghiệm nhỏ nhất của phương trình
1 x 2 + 4 x + 3 + 1 x 2 + 8 x + 15 + 1 x 2 + 12 x + 35 + 1 x 2 + 16 x + 63 = 1 5
Chọn khẳng định đúng.
A. x 0 > 0
B. x 0 < -5
C. x 0 = -10
D. x 0 > 5
Phân tích các mẫu thành nhân tử sau đó nhân cả 2 vế của phương trình với 2 ta được:
Pt tương đương:
1 ( x + 1 ) ( x + 3 ) + 1 ( x + 3 ) ( x + 5 ) + 1 ( x + 5 ) ( x + 7 ) + 1 ( x + 7 ) ( x + 9 ) = 1 5
⇔ 2 ( x + 1 ) ( x + 3 ) + 2 ( x + 3 ) ( x + 5 ) + 2 ( x + 5 ) ( x + 7 ) + 2 ( x + 7 ) ( x + 9 ) = 2 5
ĐKXĐ: x ≠ -1; -3; -5; -7; -9
Khi đó:
<=> 1 x + 1 - 1 x + 3 + 1 x + 3 - 1 x + 5 + 1 x + 5 - 1 x + 7 + 1 x + 7 - 1 x + 9 = 2 5
<=> 1 x + 1 - 1 x + 9 = 2 5
<=> 1 ( x + 9 ) - 1 ( x + 1 ) ( x + 1 ) ( x + 9 ) = 2 ( x + 1 ) ( x + 9 ) 5 ( x + 1 ) ( x + 9 )
=> 5[x + 9 – (x + 1)] = 2(x + 1) (x + 9)
ó 5(x + 9 – x – 1) = 2 x 2 + 20x + 18
ó 2 x 2 + 20x – 22 = 0
Đúng 0
Bình luận (0)
Rút gọn biểu thức:a)
P
1
(
x
−
2
y
)
2
+
1
x
2
−
4...
Đọc tiếp
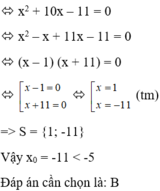
Rút gọn biểu thức:
a) P = 1 ( x − 2 y ) 2 + 1 x 2 − 4 y 2 + 1 ( x + 2 y ) 2 . x 2 + 4 xy + 4 y 2 16 x
b) Q = 1 x 2 + 8 x + 16 − 1 x 2 − 8 x + 16 : 1 x + 4 + 1 x − 4 .
a) Ta có P = 4 x 2 ( x − 2 y ) 2 ( x + 2 y ) 2 . ( x + 2 y ) 2 16 x = x 4 ( x − 2 y ) 2
Với x ≠ 0 , x ≠ ± 2 y
b) Ta có Q = 16 x ( x 2 − 16 ) 2 . x 2 − 16 2 x = 8 16 − x 2 với x ≠ 0 , x ≠ ± 4
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau:
a) (2x+12x−1−2x−12x+1):4x10x−5(2x+12x−1−2x−12x+1):4x10x−5
b) (1x2+x−2−xx+1):(1x+x−2);(1x2+x−2−xx+1):(1x+x−2);
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2).
ai làm đúng thì kết bạn với mình nha!
a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2x+1).4x=102x−18x.5(2x+1)(2x−1)(2x+1).4x=102x−1
b) (1x2+x−2−xx+1):(1x+x−2)(1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)+x−2x+1):1+x2−2xx(1x(x+1)+x−2x+1):1+x2−2xx
=1+x(x−2)x(x+1).xx2−2x+11+x(x−2)x(x+1).xx2−2x+1
=(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]
Đúng 0
Bình luận (0)
a) (2x+12x−1−2x−12x+1):4x10x−5(2x+12x−1−2x−12x+1):4x10x−5
= 0 - 0
= 0
b) (1x2+x−2−xx+1):(1x+x−2);(1x2+x−2−xx+1):(1x+x−2)
= (x-xx+1) : (2x-2) : (x-xx+1) : (2x-2)
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
= -2x-1-xx2+1. (14 - 4x)
= -x2-1-xx2+14-4x
= -6x-xx2+13
Đúng 0
Bình luận (0)
a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2x+1).4x=102x−18x.5(2x+1)(2x−1)(2x+1).4x=102x−1
b) (1x2+x−2−xx+1):(1x+x−2)(1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)+x−2x+1):1+x2−2xx(1x(x+1)+x−2x+1):1+x2−2xx
=1+x(x−2)x(x+1).xx2−2x+11+x(x−2)x(x+1).xx2−2x+1
=(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]
Đúng 0
Bình luận (0)
Cho A
x
2
+
1
3
x
:
x
2
+
1
x
−
1
:
x
3
−
1...
Đọc tiếp
Cho A = x 2 + 1 3 x : x 2 + 1 x − 1 : x 3 − 1 x 2 + x : x 2 + 2 x + 1 x 2 + x + 1 và B = x + 3 x 2 − 1 : x + 4 x 2 + 6 x − x + 3 x 2 − 1 : x + 4 x − 4 . Khi x = 101, hãy so sánh A và B.
A. B < A
B. B > A
C.B = A
D. B ≤ A
Giải phương trình:
8
x
+
1
x
2
+
4
x
2
+
1
x
2
2
x
+
4
2...
Đọc tiếp
Giải phương trình:
8 x + 1 x 2 + 4 x 2 + 1 x 2 2 = x + 4 2 + 4 x + 1 x 2 x 2 + 1 x 2
Giải phương trình chứa ẩn ở mẫu sau:
2
x
−
1
x
2
+
4
x
−
5
+
x
−
2
x
2
−
10...
Đọc tiếp
Giải phương trình chứa ẩn ở mẫu sau:
2 x − 1 x 2 + 4 x − 5 + x − 2 x 2 − 10 x + 9 = 3 x − 12 x 2 − 4 x − 45 .
giải phương trình vô tỉ sau
x2+2x.√x+1x2=8x−1
Tìm x, biết:a)
2
x
+
1
x
2
−
4
x
+
4
−
2
x
+
5
x
2
−
4...
Đọc tiếp
Tìm x, biết:
a) 2 x + 1 x 2 − 4 x + 4 − 2 x + 5 x 2 − 4 = 0 với x ≠ ± 2 ;
b) 3 x − 2 − 4 x 4 − x 2 + x x + 2 = 0 với x ≠ ± 2 ;
Chứng minh rằng: Giá trị của biểu thức
x
+
1
x
2
:
x
2
+
1
x
2
+
2...
Đọc tiếp
Chứng minh rằng: Giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
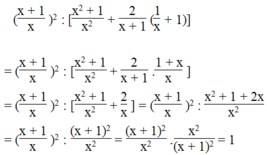
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
Đúng 0
Bình luận (0)