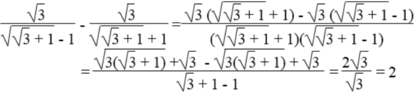33+1=

Những câu hỏi liên quan
Solution
We have: 3A = 3. (1 + 3 + 32 + 33 + ... + 399 + 3100) (1 + 3 + 32 + 33 + ... + 399 + 3100)
3A = 3 + 32 + 33 + ... + 3100 + 31013 + 32 + 33 + ... + 3100 + 3101
Inferred: 3A - A = (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100)
2A = 3101−13101−1
⇒⇒ A = 3101−123101−12
So A = 3101−12
Please help me
Dịch ra là: Ta có: 3A = 3. (1 + 3 + 32 + 33 + ... + 399 + 3100) (1 + 3 + 32 + 33 + ... + 399 + 3100) 3A = 3 + 32 + 33 + ... + 3100 + 31013 + 32 + 33 + ... + 3100 + 3101 Suy ra: 3A - A = (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) ⇒⇒ A = 3101−123101−12 Vậy A = 3101−12
Mà đoạn 2A sai nhé bạn, sửa lại:
2A = 3101−13101−1 2A=-10001
A=-10001/2
A=-5000,5
Vậy A=-5000,5
1+1=...
22+33+333+3+33+3+3+3+33+3++3+33+3+3+3+3+3+3+++11111+1111+1111++1+1=....
22+33+333+3+33+3+3+3+33+3++3+33+3+3+3+3+3+3+++11111+1111+1111++1+1=13858
Đúng 0
Bình luận (0)
1+1=2
câu 2 ko ra Kết quả vì có tới 2 dấu cộng ở cùng chỗ nên ko ra kết quả
nếu ra thì là 13855
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
câu trả lời cho câu hỏi của Huong Le Thị Lan: 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20+21+22+23+24+25+26+27+28+29+30+31+32.
=(1+32)+(2+31)+(3+30)+(4+29)+(5+28)+(6+27)+(7+26)+(8+25)+(9+24)+(10+23)+(11+22)+(12+21)+(13+20)+(14+19)+(15+18)+(16+17)
=33+33+33+33+33+33+33+33+33+33+33+33+33+33+33+33. =33.16 (dấu chấm là dấu nhân)=528
wow! mù mắt. Ido tính toán có khác!
C2:(32+1)x32:2=528
bạn tính thử xem đúng đấy.
Xem thêm câu trả lời
Rút gọn các biểu thức: 3 3 + 1 - 1 - 3 3 + 1 + 1
(x-1).(x+y)=33
Vì 33 có các ước là +1 và -1; +3 và -3: +33 và -33: +11 và -11 và x:y thuộc tập hợp Z. Nên (x-1):(x-y) là 1 số nguyên....
BẠN NÀO GIẢI ĐC GIÚP MÌNH NHA^^..CẢM ƠN NHIỀU
ta có:(x-1)(x+y) thuộc Ư(33)
ta có bảng sau:
x-1 | 1 | -1 | 3 | -3 | 11 | -11 | 33 | -33 |
X | 2 | 0 | 4 | -2 | 12 | -10 | 34 | -32 |
Y | 31 | 33 | 29 | 35 | 21 | 43 | -1 | -1 |
Tổng kết số cặp | (2;31) | (0;33) | (4;29) | (-2;35) | (12;21) | (-10;43) | (34;-1) | (-32;-1) |
Đúng 0
Bình luận (0)
Bài 1: tính tổng dãy số sau:A 1+3+32+33+...+399+3100Các bạn xem bài giải của mình nếu đúng tick cho mình nhé!GiảiTa có: 3A 3.(1+3+32+33+...+399+3100)(1+3+32+33+...+399+3100)3A 3+32+33+...+3100+31013+32+33+...+3100+3101Suy ra: 3A – A (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)(3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)2A 3101−13101−1⇒⇒ A 3101−123101−12Vậy A 3101−12
Đọc tiếp
Bài 1: tính tổng dãy số sau:
A = 1+3+32+33+...+399+3100
Các bạn xem bài giải của mình nếu đúng tick cho mình nhé!
Giải
Ta có: 3A = 3.(1+3+32+33+...+399+3100)(1+3+32+33+...+399+3100)
3A = 3+32+33+...+3100+31013+32+33+...+3100+3101
Suy ra: 3A – A = (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)(3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)
2A = 3101−13101−1
⇒⇒ A = 3101−123101−12
Vậy A = 3101−12
xin lỗi bài trên của mình làm sai
Đúng 0
Bình luận (0)
Ta có: 3A = 3.(1+3+32+33+...+399+3100)
3A = 3+32+33+...+3100+3101
Suy ra: 3A – A = (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)
2A = 3101−1
⇒ A = 3101−1
2
Vậy A = 3101−1
2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính nhanh
1/33 x ( 33/12+33/2020+333333/303030+33333333/42424242)
Sửa đề:
\(\frac{1}{33}\times\left(\frac{33}{12}+\frac{3333}{2020}+\frac{333333}{303030}+\frac{33333333}{42424242}\right)\)
\(=\frac{1}{33}\times\frac{33}{12}+\frac{1}{33}\times\frac{3333}{2020}+\frac{1}{33}\times\frac{333333}{303030}+\frac{1}{33}\times\frac{33333333}{42424242}\)
\(=\frac{1}{12}+\frac{33\times101}{33\times101\times20}+\frac{33\times10101}{33\times10101\times30}+\frac{33\times1010101}{33\times1010101\times42}\)
\(=\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}\)
\(=\frac{1}{3x4}+\frac{1}{4x5}+\frac{1}{5x6}+\frac{1}{6x7}\)
\(=\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}\)
\(=\frac{1}{3}-\frac{1}{7}\)
\(=\frac{4}{21}\)
Đúng 0
Bình luận (0)
* Tính :
a) A = 1/3 + 1/15 + 1/35 + 1/63 + 1/99
b) B = 7/4 . ( 33/12 + 33/20 + 33/30 + 33/42 + 33/56 )
c) C = 1/1.3 + 1/3.5 + 1/5.7 + ... + 1/2013.2019
d) D = 3^2/1.4 + 3^2/4.7 + 3^2/7.10 + 3^2/10.13 + 3^2/13.16
* Cho abc = 105, bc + b + 1 khác 0. Tính : S = 105/abc + ab + a + b/bc + b + 1 + a/ab + a + 105
A= \(\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+\frac{1}{35}+\frac{1}{99}=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\frac{1}{9.11}\)
\(2A=\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.6}+...+\frac{2}{9.11}\)
\(2A=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{11}\)
\(2A=1-\frac{1}{11}=\frac{10}{11}\)
\(A=\frac{10}{11}:2=\frac{5}{11}\)
Đúng 0
Bình luận (0)
\(D=\frac{3^2}{1.4}+\frac{3^2}{4.7}+...+\frac{3^2}{13.16}\)
\(D=3.\left(\frac{3}{1.4}+\frac{3}{4.7}+...+\frac{3}{13.16}\right)\)
\(D=3.\left(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+...+\frac{1}{13}-\frac{1}{16}\right)\)
\(D=3.\left(1-\frac{1}{16}\right)=3.\frac{15}{16}=2\frac{13}{16}\)
Đúng 0
Bình luận (0)
33/33+88/44-1=?
\(\frac{33}{33}+\frac{88}{44}-1\)
\(=1+\frac{88}{44}-1\)
\(=1+2-1\)
\(=2\)
Đúng 0
Bình luận (0)
33/33 + 88/44 - 1
= 1 + 2 - 1
= (1 - 1) + 2
= 0 + 2
= 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
(5x-1/2 )nhan (3x+1 )
Xem chi tiết
\(\left(5x-\frac{1}{2}\right)\left(3x+1\right)\)
\(=15x^2+5x-\frac{3}{2}x-\frac{1}{2}\)
\(=15x^2+\frac{7}{2}x-\frac{1}{2}\)
Ủng hộ nhé
Đúng 0
Bình luận (0)