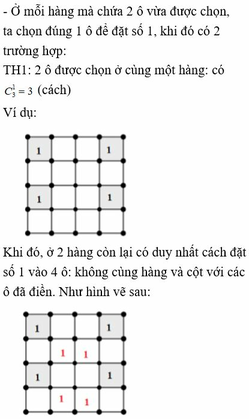
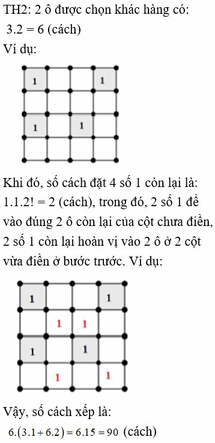
Cho lưới ô vuông 5.5. Người ta điền vào các ô của lưới một trong các số -1;0;1. Xét tổng các số đó tính theo từng cột tửng hàng từng đường chéo. Chứng minh rằng luôn tồn tại 2 tổng có giá trị bằng nhau

Những câu hỏi liên quan
Cho lưới ô vuông 5.5. Người ta điền vào các ô của lưới một trong các số -1;0;1. Xét tổng các số đó tính theo từng cột tửng hàng từng đường chéo. Chứng minh rằng luôn tồn tại 2 tổng có giá trị bằng nhau
Cho một lưới ô vuông kích thước 5x5.Người ta điền vào mỗi ô của lưới một trong các số -1;0;1.Xét tổng của các ô được tính theo từng cột,theo từng hàng và theo từng đường chéo.Hãy chứng tỏ rằng trong tất cả các tổng đó luôn tồn tại hai tổng có giá trị bằng nhau.
Cho lưới ô vuông 6x6. Người ta điền vào mỗi ô vuông một trong các số -1; 0; 1. Xét tổng các số được tính theo hàng, theo cột, theo từng đường chéo. chứng minh rằng luôn tồn tại hai tổng có giá trị bằng nhau.
Kí hiệu \(S\) là tổng tất cả các số trên cùng 1 hàng, cột hay đường chéo. Dễ dàng kiểm chứng được \(-6\le S\le6\). Ta thấy từ \(-6\) đến \(6\) có tất cả là 13 số nguyên. Nói cách khác, sẽ có tất cả 13 giá trị khác nhau mà \(S\) có thể đạt được. Do trên bảng 6x6 có 6 cột, 6 hàng, 2 đường chéo ứng với 14 tổng S nên theo nguyên lí Dirichlet, sẽ tồn tại 2 tổng S mang cùng 1 giá trị, đây là đpcm.
Đúng 2
Bình luận (0)
Trong một lưới ô vuông kích thước \(5.5\), người ta điền ngẫu nhiên vào các ô một trong các giá trị −1, 0 hoặc 1, sau đó tính tổng tất cả các ô theo hàng ; theo cột và theo hai đường chéo. Chứng minh rằng tồn tại ít nhất hai tổng có giá trị bằng nhau.
Cho một lưới vuông kích thước 5x5. Người ta điền vào mỗi ô của lưới một trong các số -1 ; 0 ; 1. Xét tổng các số được tính theo từng cột, theo từng hàng và theo từng đường chéo. Hãy chứng tỏ rằng trong tất cả các tổng đó luôn tồn tại hai tổng đó luôn tồn tại hai tổng có giá trị bằng nhau.
giúp tớ với !
Cho lưới ô vuông3x3 Ta điền vào ô trống một trong các số :-1,1,0 xét tổng các số được tính theo hàng cột và theo đường chéo . Cmr luôn có một tồn tại một tổng
Cho một bảng hình vuông kích thước n nhân n được chia thành lưới ô vuông đơn vị, các vị trí đỉnh của các ô vuông đơn vị được gọi là các mắt lưới. Người ta muốn đếm số lượng những hình vuông thỏa mãn hai điều kiện sau: Mỗi cạnh hình vuông phải song song với một trong hai cạnh bảng; Cả 4 đỉnh của hình vuông phải nằm tại vị trí của các mắt lưới. Ví dụ với bảng kích thước 3 nhân 3 ta có thể đếm được 14 hình vuông thỏa mãn hai điều kiện trên.Tìm số hình vuông trên.
Đọc tiếp
Cho một bảng hình vuông kích thước n nhân n được chia thành lưới ô vuông đơn vị, các vị trí đỉnh của các ô vuông đơn vị được gọi là các mắt lưới. Người ta muốn đếm số lượng những hình vuông thỏa mãn hai điều kiện sau: Mỗi cạnh hình vuông phải song song với một trong hai cạnh bảng; Cả 4 đỉnh của hình vuông phải nằm tại vị trí của các mắt lưới. Ví dụ với bảng kích thước 3 nhân 3 ta có thể đếm được 14 hình vuông thỏa mãn hai điều kiện trên.
Tìm số hình vuông trên.
Cho một bảng hình vuông kích thước 𝑛 × 𝑛 được chia thành lưới ô vuông đơn vị, các vị trí đỉnh của các ô vuông đơn vị được gọi là các mắt lưới. Hãy đếm số những hình vuông thỏa mãn hai điều kiện sau: Mỗi cạnh hình vuông phải song song với một trong hai cạnh bảng. Cả 4 đỉnh của hình vuông phải nằm tại vị trí của các mắt lưới.
Xét một bảng ô vuông gồm
4
×
4
ô vuông. Người ta điền vào mỗi ô vuông một trong hai số 1 hoặc 1 sao cho tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0. Hỏi có bao nhiêu cách điền số?
Đọc tiếp
Xét một bảng ô vuông gồm 4 × 4 ô vuông. Người ta điền vào mỗi ô vuông một trong hai số 1 hoặc 1 sao cho tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0. Hỏi có bao nhiêu cách điền số?
![]()
![]()
![]()
![]()