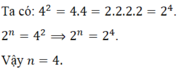Số tụ nhiên n thỏa mãn 2n = 32 là n =

Những câu hỏi liên quan
số tự nhiên n thỏa mãn 2n=32 là n= ...
cho n là số tụ nhiên khác 0
số giá trị của x thỏa mãn \(\left(3x^2-51\right)^{2n}=\left(-24\right)^{2n}\) là
Số tự nhiên n thỏa mãn 2 n = 4 2 là:
A. n = 3
B. n = 4
C. n = 5
D. n = 6
Số số tự nhiên n thỏa mãn: 3 (n+1)⋮(2n + 3) là ?
Tìm số tự nhiên n thỏa mãn : \(4^{n+3}+17.2^{2n}=9^{n+1}+7.3^{2n}\)
Tập hợp các số tự nhiên n thỏa mãn là {...}
(nếu có nhiều phần tử , nhập theo thứ tự tăng dần , cách nhau bởi dấu ";")
Ta có
\(\frac{4^{n+3}+17.2^{2n}}{9^{n+1}+7.3^{2n}}=\frac{2^{2n+6}+17.2^{2n}}{3^{2n+2}+7.3^{2n}}=\frac{2^{2n}.\left(2^6+17\right)}{3^{2n}.\left(3^2+7\right)}=\left(\frac{2}{3}\right)^{2n}.\frac{81}{16}=1\)
\(\Rightarrow\left(\frac{2}{3}\right)^{2n}.\frac{3^4}{2^4}=1\Rightarrow\left(\frac{2}{3}\right)^{2n}=\left(\frac{2}{3}\right)^4\Rightarrow2n=4\Rightarrow n=2\)
Đúng 0
Bình luận (0)
Số tự nhiên n thỏa mãn (2+4+6+...+2n)=210 là n=
Cón số nên (2+2n).n/2=210
(1+n).n=210
n=14
Đúng 0
Bình luận (0)
Số tự nhiên n lớn nhất thỏa mãn : (2n + 12) : (n – 1) là :
Để 2n + 12 chia hết n-1
Hay 2n - 2 + 14 chia hết n-1
n-1 = 14
n=15
Đúng 0
Bình luận (0)
(2n+12) chia hết cho (n-1) ĐK: n ≥ 1
=> [(2n-2)+14] chia hết cho (n-1)
=> [2(n-1)+14] chia hết cho (n-1)
Vì 2(n-1) chia hết cho (n-1) nên 14 chia hết cho (n-1)
Để n lớn nhất thì n-1 phải lớn nhất
=> (n-1) ∈ Ư(14) và n-1 lớn nhất
=> n-1=14
=> n=15
Vậy n=15
Đúng 0
Bình luận (0)
:
(2n+12) chia hết cho (n-1) ĐK: n ≥ 1
=> [(2n-2)+14] chia hết cho (n-1)
=> [2(n-1)+14] chia hết cho (n-1)
Vì 2(n-1) chia hết cho (n-1) nên 14 chia hết cho (n-1)
Để n lớn nhất thì n-1 phải lớn nhất
=> (n-1) ∈ Ư(14) và n-1 lớn nhất
=> n-1=14
=> n=15
Vậy n=15
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên n thỏa mãn 4n+3 +17.22n
Trả lời: Tập hợp số tự nhiên n thỏa mãn là { }.
Số tự nhiên n thỏa mãn: (3n + 1)⋮(2n + 3) là ...
3n+1 chia hết cho 2n+3
=> 6n+2 chia hết cho 2n+3
=> 6n+9-7 chia hết cho 2n+3
Vì 6n+9 chia hết cho 2n+3
=> -7 chia hết cho 2n+3
=> 2n+3 thuộc Ư(-7)
| 2n+3 | n |
| 1 | -1 |
| -1 | -2 |
| 7 | 2 |
| -7 | -5 |
Mà n là số tự nhiên
=> n = 2
Đúng 0
Bình luận (0)