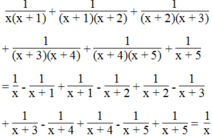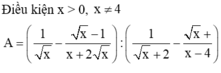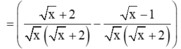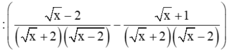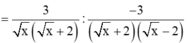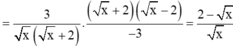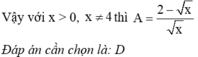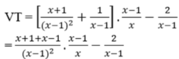1x.2x=366

Những câu hỏi liên quan
Giải các phương trình sau:a)
x
−
2
x
+
x
x
+
2
2
;
b)
2
x
+
1
−
1
x
−
2
3...
Đọc tiếp
Giải các phương trình sau:
a) x − 2 x + x x + 2 = 2 ;
b) 2 x + 1 − 1 x − 2 = 3 x − 11 x + 1 x − 2 ;
c) 5 + 96 x 2 − 16 = 2 x − 1 x + 4 + 3 x − 1 x − 4 ;
d) 2 x + 2 − 2 x 2 + 16 x 3 + 8 = 5 x 2 − 2 x + 4 .
Giải các phương trình sau
1
-
2
x
-
1
x
+
1
3
+
6
1
-
2
x
-...
Đọc tiếp
Giải các phương trình sau 1 - 2 x - 1 x + 1 3 + 6 1 - 2 x - 1 x + 1 2 = 12 2 x - 1 x + 1 - 20
Đặt y = 1 - 2 x - 1 x + 1 , ta có:
12 2 x - 1 x + 1 - 20 = - 12 1 - 2 x - 1 x + 1 - 8 = - 12 y - 8
Do đó phương trình đã cho có dạng y 3 + 6 y 2 = −12y − 8
Giải phương trình này:
y 3 + 6 y 2 = −12y − 8
⇔ y 3 + 3 y 2 .2 + 3y. 2 2 + 2 3 = 0
⇔ y + 3 3 = 0
⇔y =−2
Vậy phương trình đã cho tương đương với phương trình
1 - 2 x - 1 x + 1 = - 2 h a y 2 x - 1 x + 1 = 3
ĐKXĐ của phương trình là x ≠ -1. Giải phương trình này bằng cách khử mẫu, ta được:
2x − 1 = 3(x + 1)
⇔x = −4
Giá trị x = -4 thỏa mãn ĐKXĐ nên là nghiệm của phương trình đã cho.
Đúng 0
Bình luận (0)
Chứng minh:
1
x
x
+
1
+
1
x
+
1
x
+
2
+
1
x
+
2...
Đọc tiếp
Chứng minh:
1 x x + 1 + 1 x + 1 x + 2 + 1 x + 2 x + 3 + 1 x + 3 x + 4 + 1 x + 4 x + 5 + 1 x + 5
Cho biểu thức
A
1
x
-
x
-
1
x
+
2
x
:
1
x
+
2...
Đọc tiếp
Cho biểu thức A = 1 x - x - 1 x + 2 x : 1 x + 2 - x + 1 x - 4
A. A = x - 2 x
B. A = 2 + x x
C. A = 2 - x 2 x
D. A = 2 - x x
Giải phương trình:
3
x
-
1
x
-
2
+
2
x
...
Đọc tiếp
Giải phương trình: 3 x - 1 x - 2 + 2 x - 3 x - 1 = 1 x - 2 x - 3
Điều kiện xác định: x ≠ 1; x ≠ 2; x ≠ 3.
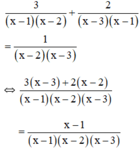
⇒ 3(x – 3) + 2(x – 2) = x – 1
⇔ 3x – 9 + 2x – 4 = x – 1
⇔ 3x + 2x – x = 9 + 4 – 1
⇔ 4x = 12
⇔ x = 3 (không thỏa mãn điều kiện xác định)
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Đố. Đố em tính nhanh được tổng sau:
1
x
x
+
1
+
1
x
+
1
x
+
2...
Đọc tiếp
Đố. Đố em tính nhanh được tổng sau:
1 x x + 1 + 1 x + 1 x + 2 + 1 x + 2 x + 3 + 1 x + 3 x + 4 + 1 x + 4 x + 5 + 1 x + 5 x + 6
Áp dụng kết quả Bài 31 a) (trang 50 SGK Toán 8 Tập 1) ta được:
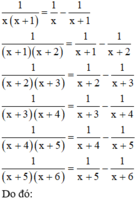
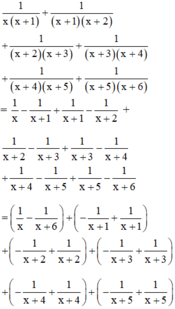
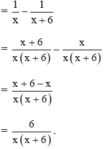
Đúng 0
Bình luận (0)
Rút gọn biểu thức P = x − 2 x + 2 x − 1 x + 1 x + 2 , x > 0
P = x − 2 x + 2 x − 1 x + 1 x + 2 , x > 0
P = x − 2 − x + 2 + x x x + 2 = x − 4 x x + 2 = x − 2 x
Đúng 0
Bình luận (0)
Giải phương trình
1
x
-
1
+
x
2
-
2
x
+
5
+
1
x
-
1
-
x
2...
Đọc tiếp
Giải phương trình 1 x - 1 + x 2 - 2 x + 5 + 1 x - 1 - x 2 - 2 x + 5 = 1
A. x = −2
B. x = 0
C. x = 1
D. x = −1
Chứng minh rằng:
x
+
1
x
-
2
x
+
1
+
1
x
-
1
:
x
x
-
1
-...
Đọc tiếp
Chứng minh rằng:
x + 1 x - 2 x + 1 + 1 x - 1 : x x - 1 - 2 x - 1 = 0