Cho hình tam giác to chia hình đó thành 10 hình tam giác nhỏ

Những câu hỏi liên quan
cho hình tam giác abc. hỏi có bao nhiêu cách để chia hình tam giác abc thành 3 hình tam giác nhỏ có diện tích bằng nhau
Xem thêm câu trả lời
cho hình tam giác abc. hỏi có bao nhiêu cách để chia hình tam giác abc thành 3 hình tam giác nhỏ có diện tích bằng nhau
1. Cho tam giác ABC. Hãy vẽ ra các cách chia hình tam giác đó thành ba hình tam giác có diện tích bằng nhau
2. Cho tam giác ABC với một đường thẳng. Hãy chia tam giác ABC thành 2 hình tam giác sao cho hình này gấp 2 lần diện tích hình kia
Xếp bốn hình tam giác nhỏ thành hình tam giác to (xem hình vẽ) :
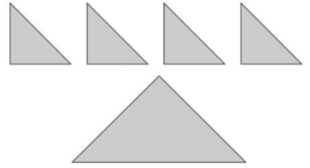
Phương pháp giải:
- Chia hình cần xếp thành 4 hình tam giác có kích thước bằng hình đã cho.
- Xếp 4 hình tam giác nhỏ theo cách chia vừa làm ở bước trên.
Lời giải chi tiết:
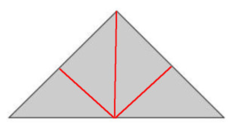
Đúng 0
Bình luận (0)
Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.
Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.Cho hình thang ABCD(AB//CD) đường chéo BD chia hình thang thành 2 tam giác cân. Tam giác ABD cân tại A. Tam giác BCD cân tại B. Tính các góc của hình thang cân đó.
Trong hình thang cân ABCD (AB//CD) đặt m là sđ góc D (m<180 độ ) thì:D=C=m và A=B=180 độ-m
Tam giác ABD cân tại A =>^ABD=^ADB
AB//CD tạo với cát tuyến BD 2 góc so le trong ^ABD=^CDB
Suy ra ^ADB=^CDB,lại có tia DB nằm giữa 2 tia DA và DC nên tia DB là tia phân giác ^ADC=m độ
Vậy ^ABD= (1/2).m
Tam giác BCD cân tại D =>^DBC=^DCB=m độ
Tia BD nằm giữa 2 tia BA,BC nên ^ABC=^ABD+^DBC=(1/2).m+m (độ)
=(3/2).m (độ)
Mà ^ABC=180-m (độ),nên (3/2).m(độ)=180-m(độ)
hay 5/2.m=180 độ => m=360độ:5=72 độ
và 180 độ-m=108 độ
Trả lời : Trong hình thang cân ABCD kể trên,sđ 2 góc nhọn C và D là 72 độ,sđ 2 góc còn lại là 108 độ
Đúng 1
Bình luận (0)
cho hình tam giác abc. hãy vẽ các cách chia tam giác đó thành 3 hình tam giác có diện tích bằng nhau
kkkkgggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg
a) Cách vẽ :
Lấy BD=DE=EC= 12BC.
Nối AD và AE.
b) Giải thích:
SABD = SADE = SAEC = 12 SABC
Chia một hình tam giác đều thành các tam giác đều nhỏ hơn, hỏi có ít nhất là bao nhiêu tam giác đều nhỏ?
( bài này không có hình )
Cho hình thang ABCD có diện tích 12,6cm2 đường chéo AC chia hình thành hai hình tam giác , trong đó diện tích hình tam giác ABC bằng 3/4 diện tích hình tam giâc ACD. Tính diện tích của mỗi hình tam giac đó
Tổng số phần bằng nhau là :
3 + 4 = 7 ( phần )
Diện tích hình tam giác ABC là :
12,6 : 7 x 3 = 5,4 ( cm2 )
Diện tích hình tam giác ACD là :
12,6 - 5,4 = 7,2 ( cm2 )
Đáp số : tam giác ABC : 5,4 cm2
tam giác ACD : 7,2 cm2
Đúng 0
Bình luận (0)
Cho một hình thang vuông có đáy lớn bằng 3 m, đáy nhỏ và chiều cao bằng 2 m. Hãy chia hình thang đó thành 5 hình tam giác có diện tích bằng nhau. Hãy tìm các kiểu chia khác nhau sao cho số đo chiều cao cũng như số đo đáy của tam giác đều là những số tự nhiên.
Bài giải:
Diện tích hình thang là:
(3 + 2) x 2 : 2 = 5 (m2)
Chia hình thang đó thành 5 tam giác có diện tích bằng nhau thì diện tích một tam giác là : 5 : 5 = 1 (m2). Các tam giác này có chiều cao và số đo đáy là số tự nhiên nên nếu chiều cao là 1m thì đáy là 2 m. Nếu chiều cao là 2 m thì đáy là 1 m. Có nhiều cách chia, TTT chỉ nêu một số cách chia sau: vào "câu hỏi tương tự"
Đúng 0
Bình luận (0)
Diện tích hình thang là:
(3 + 2) x 2 : 2 = 5 (m2)
Chia hình thang đó thành 5 tam giác có diện tích bằng nhau thì diện tích một tam giác là : 5 : 5 = 1 (m2). Các tam giác này có chiều cao và số đo đáy là số tự nhiên nên nếu chiều cao là 1m thì đáy là 2 m.
Đúng 0
Bình luận (0)



















