1
a2
Những câu hỏi liên quan
0,5+(87-1a2)=45
0,5 +(87-1a2)=45
87-1a2=45-0,5
87-1a2=44,5
1a2=87-44,5
1a2=42,5
1a =42,5:2
1a =21,25
a=21,5
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Điền dấu thích hợp vào ô trống: 1a2 + a30 +41a......aaa 540
Cho a, b, c 0 a b c 1.Tìm GTNN của 1a2 b2 c2 1abc
Xem chi tiết
bn cs thể ghi rõ đề đc ko?
Giải hệ phương trình
x
+
3
y
1
a
2
+
1
x
+
6...
Đọc tiếp
Giải hệ phương trình x + 3 y = 1 a 2 + 1 x + 6 y = 2 a trong mỗi trường hợp sau: a = 1
Cách 1
Ta có: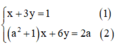 
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được :
(a2 + 1).(1 – 3y) + 6y = 2a
⇔ a2 + 1 – 3(a2 + 1)y + 6y = 2a
⇔ a2 +1- 2a = 3a2.y – 6y + 3y
⇔ ( a- 1)2 = 3a2y – 3y
⇔ 3(a2 – 1).y = (a – 1)2 (**)
a = 1, phương trình (**) trở thành: 0y = 0
Phương trình nghiệm đúng với mọi y.
Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1 – 3y; y) (y ∈ R).
Thay a=1 vào hệ phương trình ta được hệ phương trình mới:
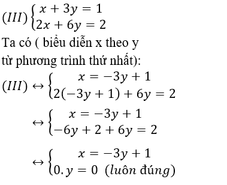
Vậy với a= 1 hệ phương trình có vô số nghiệm với nghiệm tổng quát là (-3y+1;y),(y ∈ R
Đúng 0
Bình luận (0)
Giải hệ phương trình
x
+
3
y
1
a
2
+
1
x
+
6...
Đọc tiếp
Giải hệ phương trình x + 3 y = 1 a 2 + 1 x + 6 y = 2 a trong mỗi trường hợp sau: a = -1
Cách 1
Ta có: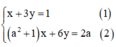 
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được :
(a2 + 1).(1 – 3y) + 6y = 2a
⇔ a2 + 1 – 3(a2 + 1)y + 6y = 2a
⇔ a2 +1- 2a = 3a2.y – 6y + 3y
⇔ ( a- 1)2 = 3a2y – 3y
⇔ 3(a2 – 1).y = (a – 1)2 (**)
a = -1, phương trình (**) trở thành : 0y = 4
Phương trình trên vô nghiệm
Vậy hệ phương trình khi a = -1 vô nghiệm.
Cách 2
Thay a = -1 vào hệ phương trình ta được hệ phương trình mới:
Vậy hệ phương trình vô nghiệm khi a= - 1.
Đúng 0
Bình luận (0)
Giải hệ phương trình
x
+
3
y
1
a
2
+
1
x
+
6...
Đọc tiếp
Giải hệ phương trình x + 3 y = 1 a 2 + 1 x + 6 y = 2 a trong mỗi trường hợp sau: a = 0
Cách 1
Ta có: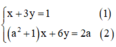 
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được :
(a2 + 1).(1 – 3y) + 6y = 2a
⇔ a2 + 1 – 3(a2 + 1)y + 6y = 2a
⇔ a2 +1- 2a = 3a2.y – 6y + 3y
⇔ ( a- 1)2 = 3a2y – 3y
⇔ 3(a2 – 1).y = (a – 1)2 (**)
a = 0, phương trình (**) trở thành -3y = 1 ⇔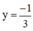 
Thay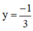 
vào (*) ta được x = 2.
Vậy hệ phương trình khi a = 0 có nghiệm duy nhất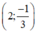 
Thay a = 0 vào hệ phương trình ta được hệ phương trình mới:
Đúng 0
Bình luận (0)
Đạo hàm của hàm số:
f
x
x
2
+
1
a
2
+
x
2
(a là hằng số) bằng biểu thức nào sau đây? A.
2
x
a
2...
Đọc tiếp
Đạo hàm của hàm số: f x = x 2 + 1 a 2 + x 2 (a là hằng số) bằng biểu thức nào sau đây?
A. 2 x a 2 - x 2
B. x ( 3 x 2 + 2 a 2 + 1 ) ( a 2 + x 2 ) . a 2 + x 2
C. 2 x 2 a - 2 x
D. x 2 a 2 - x 2 + 1 a 2 - x 2 a 2 - x 2
Chọn B
y ' = 2 x . a + 2 x 2 + ( x 2 + 1 ) . 1 2 a 2 + x 2 . ( a 2 + x 2 ) ' a 2 + x 2 = 2 x . a + 2 x 2 + x ( x 2 + 1 ) a 2 + x 2 a 2 + x 2 = 2 x ( a 2 + x 2 ) + x ( x 2 + 1 ) ( a 2 + x 2 ) . a 2 + x 2 = x ( 3 x 2 + 2 a 2 + 1 ) ( a 2 + x 2 ) . a 2 + x 2
Đúng 0
Bình luận (0)
Cho phương trình ẩn x:
x
+
a
a
-
x
+
x
-
a
a
+
x
a
3
a
+
1...
Đọc tiếp
Cho phương trình ẩn x: x + a a - x + x - a a + x = a 3 a + 1 a 2 - x 2
Giải phương trình khi a = 1
Khi a = 1, ta có phương trình:
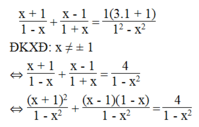
⇔ x + 1 2 + (x – 1)(1 – x) = 4
⇔ x 2 + 2x + 1 + x – x 2 – 1 + x = 4
⇔ 4x = 4 ⇔ x = 1 (loại)
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Cho phương trình ẩn x:
x
+
a
a
-
x
+
x
-
a
a
+
x
a
3
a
+
1...
Đọc tiếp
Cho phương trình ẩn x: x + a a - x + x - a a + x = a 3 a + 1 a 2 - x 2
Giải phương trình khi a = - 3
Khi a = - 3, ta có phương trình:
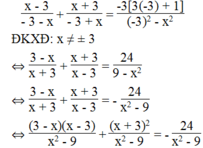
⇔ (3 – x)(x – 3) + x + 3 2 = -24
⇔ 3x – 9 – x 2 + 3x + x 2 + 6x + 9 = -24 ⇔ 12x = - 24
⇔ x = -2 (thỏa mãn)
Vậy phương trình có nghiệm x = -2
Đúng 0
Bình luận (0)
Cho phương trình ẩn x:
x
+
a
a
-
x
+
x
-
a
a
+
x
a
3
a
+
1...
Đọc tiếp
Cho phương trình ẩn x: x + a a - x + x - a a + x = a 3 a + 1 a 2 - x 2
Giải phương trình khi a = 0
Khi a = 0, ta có phương trình:
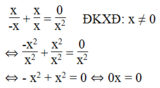
Phương trình nghiệm đúng với mọi giá trị của x ≠ 0
Vậy phương trình có nghiệm x ∈ R / x ≠ 0.
Đúng 0
Bình luận (0)