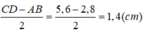cho hình thang ABCD. 2 đường chéo AC và BD cắt nhau tại O. M là điểm chính giữa đáy nhỏ AB. On và CD cắt nhau tại N. so sánh CN và ND

Những câu hỏi liên quan
cho hình thang ABCD. 2 đường chéo AC và BD cắt nhau tại O. M là điểm chính giữa đáy nhỏ AB. MO cắt CD tại N so sánh điện tích AMND và MBCN
Xem chi tiết
Vẽ hình minh họa.......
Ta xét :
Với cách chia đầu tiên,hai htg ABC và ADC là 2 htg = nhau vì chung đáy và chiều cao . Điểm M đi qua điểm O cũng tức là chia hình thang ABCD thành 2 hình thang nhỏ= nhau
KẾT LUẬN...............................................
Cho hình thang ABCD đáy nhỏ AB bằng 4cm. DC bằng 6cm. Hai đường chéo AC và BD cắt nhau tại O. Cho biết diện tích tam giác AOD bằng 9 cm2.
a, Tính diện tích hình thang ABCD
b, Gọi E là điểm chính giữa của đáy CD, nối E và O kéo dài cắt CD tại F
So sánh diện tích của tứ giác AFED với EFBC
Cho hình thang cân ABCD đáy AB, CD có 2 đường chéo AC và BD cắt nhau tại O. Gọi M và N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 12cm. a/ Tính độ dài MN và đáy nhỏ AB. b/ So sánh độ dài MN với nửa hiệu độ dài của CD và AB.
Cho hình thang abcd có đáy ab và cd. ac và bd cắt nhau tại o. Các cạnh bên kéo dài cắt nhau tại k .Đường thẳng ko cắt ab tại m, cắt cd tại n. So sánh ma và mb, nd,nc. giúp mình với mình đang cần gấp
Cho hình thang cân ABCD,AC và BD cắt nhau tại O. Gọi M,N theo thứ tự là trung điểm của các đường chéo BD,AC. Biết MD=3MO, đáy lớn CD= 5.6cm.
a,Tính độ dài đoạn thẳng MN và đáy nhỏ AB.
b,So sánh MN và nửa hiệu của CD và AB
Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. So sánh độ dài đoạn thẳng MN với nửa hiệu của CD và AB
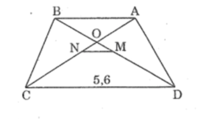
Cho hình thang ABCD (AB là đáy nhỏ, CD là đáy lớn). Đoạn thẳng AC và BD cắt nhau tại điểm O. Trên đoạn thẳng AB lấy điểm M sao cho AM = BM. Đường thẳng MO cắt đáy lớn CD ở điểm N. Chứng tỏ rằng NC = ND
Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: 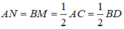
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: 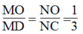
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: 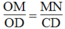 Hệ quả định lí Ta-lét)
Hệ quả định lí Ta-lét)
Suy ra: 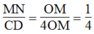
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
![]() (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra: ![]()
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
Đúng 0
Bình luận (0)
Cho hình thang ABCD đáy nhỏ AB=4cm,DC=9cm.Hai đường chéo AC và BD cắt nhau tại O.Cho biết diện tích tam giac AOD là 9cm vuông.
a.Tính diện tích hình thang ABCD
b,E là điểm chính giữa của đáy CD.nối Evà O cắt AB tại F.SO SÁNH các diện tích tứ giác AFED VA EFBC?