A² = ab - ac

A² = a(b - c)

A² = (-5).20

A² = -100

Mà A² > 0 với mọi A => Không tồn tại A.

Vậy...

Hoặc A = -5 (đề bài)

(a+b+c)²=a²+b²+c²+2(ab+bc+ca)

Thay số trên vào ta được:

9²=53+2(ab+bc+ca)

2(ab+bc+ca)=81-53

ab+bc+ca = 14

cảm ơn nha , câu này trong violympic toán , mình làm mãi ko ra!!

\(\text{(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca) }\)

\(\text{Thay số trên vào ta được: }\)

\(\text{9^2=53+2(ab+bc+ca)}\)

\(\text{2(ab+bc+ca)=81-53}\)

\(\text{ab+bc+ca = 14 }\)

a) Ta có: \(A\left(x\right)=ax^2+bx+c\)

Thay \(A\left(-1\right)\)  ta được:

\(A\left(-1\right)=a\left(-1\right)^2+b\left(-1\right)+c=a+c-b\)

\(=b-8-b=-8\)

b) \(\left\{{}\begin{matrix}A\left(0\right)=4\\A\left(1\right)=9\\A\left(2\right)=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=4\\a+b+c=9\\4a+2b+c=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=4\\a+b=5\\4a+2b=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=4\\a+b=5\\2a+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=4\\a=0\\b=5\end{matrix}\right.\)

c) 

Ta có: \(\left\{{}\begin{matrix}A\left(2\right)=4a+2b+c\\A\left(-1\right)=a-b+c\end{matrix}\right.\)

\(\Leftrightarrow A\left(2\right)+A\left(-1\right)=5a+b+2c=0\)

\(\Leftrightarrow A\left(2\right)=-A\left(-1\right)\)

\(\Leftrightarrow A\left(2\right)\times A\left(-1\right)=-\left[A\left(2\right)\right]^2\le0\)

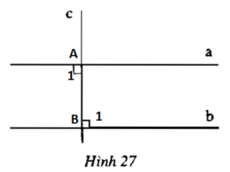
∠A1 và ∠B1 là hai góc so le trong và ∠A1 = ∠B1 = 900 nên theo dấu hiệu nhận biết a//b

\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\Rightarrow ab+bc+ca=0\)

\(a+b+c=1\Rightarrow\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)=1\)

\(\Rightarrow a^2+b^2+c^2=1\)

dung la may dua hoc ngu nhu bo