Theo qui tắc đổi dấu ta có - A B = A - B
- 4 x + 1 5 - x = . . .
Do đó ta cũng có 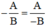
Chẳng hạn, phân thức đối của 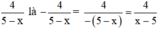
Áp dụng điều này hãy điền những phân thức thích hợp vào những chỗ trống dưới đây:
Theo qui tắc đổi dấu ta có - A B = A - B tính - x 2 + 2 1 - 5 x = . . . = . . . ;
(a + b) . ( a + b) - ( a - b) . ( a - b)
Qui tắc dấu ngoặc
Nhanh cần gấp
(a+b).(a+b) - (a-b).(a-b)
= (a+b).(a+b) + (a+b).(a-b)
= (a+b).(a+b+a-b)
= (a+b).2a
Qui đồng mẫu thức các phân thức sau (có thể áp dụng qui tắc đổi dấu với các phân thức để tìm mẫu thức chung thuận tiện hơn):
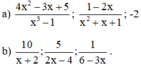
a) + Phân tích mẫu thức thành nhân tử để tìm nhân tử chung:
x3 – 1 = (x – 1)(x2 + x + 1)
x2 + x + 1 = x2 + x + 1
⇒ MTC = (x – 1)(x2 + x + 1) = x3 – 1
+ Nhân tử phụ : (Có thể bỏ qua bước này nếu đã quen)
(x3 – 1) : (x3 – 1) = 1
(x3 – 1) :( x2 + x + 1) = x - 1
(x3 – 1) : 1 = x3 – 1
+ Quy đồng :
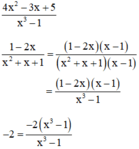
b) Ta có:
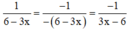
+ Phân tích mẫu thức thành nhân tử để tìm MTC
x + 2 = x + 2
2x – 4 = 2.(x – 2)
3x – 6 = 3.(x – 2)
⇒ MTC = 6.(x + 2)(x – 2)
+ Nhân tử phụ: (Có thể bỏ qua bước này nếu đã quen)
6(x + 2)(x – 2) : (x + 2) = 6(x – 2)
6(x + 2)(x – 2) : 2(x – 2) = 3(x + 2)
6(x + 2)(x – 2) : 3(x – 2) = 2(x + 2)
+ Quy đồng:
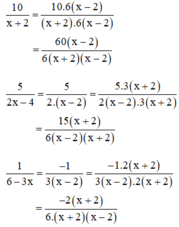
Áp dụng qui tắc đổi dấu để các phân thức có cùng mẫu thức rồi làm tính cộng phân thức:
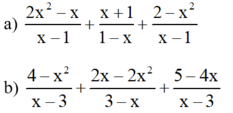
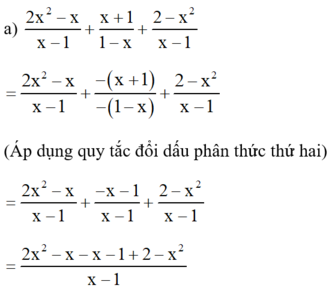
(Cộng các tử thức với nhau, giữ nguyên mẫu thức)
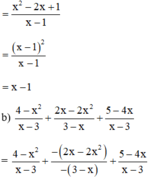
(Áp dụng quy tắc đổi dấu phân thức thứ hai)
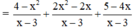
(Cộng các phân thức cùng mẫu thức)
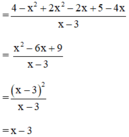
Áp dụng qui tắc đổi dấu rồi rút gọn phân thức:
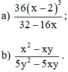
Áp dụng qui tắc đổi dấu rồi rút gọn phân thức:
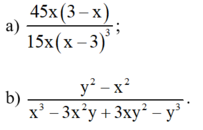
Dùng qui tắc đổi dấu rồi thực hiện các phép tính: 1 x - 5 x 2 - 25 x - 15 25 x 2 - 1
Dùng qui tắc đổi dấu rồi thực hiện các phép tính:
4 x + 13 5 x ( x - 7 ) - x - 48 5 x 7 - x
4 x + 13 5 x ( x - 7 ) - x - 48 5 x 7 - x

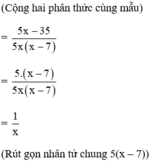
Dùng qui tắc đổi dấu rồi thực hiện các phép tính:
4 x + 13 5 x ( x - 7 ) - x - 48 5 x 7 - x