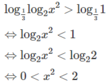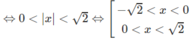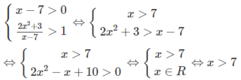Giải các phương trình logarit sau: log 4 x + 2 x + 3 + log 4 x - 2 x + 3 = 2

Những câu hỏi liên quan
Giải Phương trình logarit sau :
Log3(x2+x+1) - Log33x = 2x - x2-1
Giải các phương trình logarit sau:
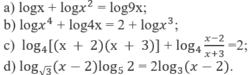
a) Với điều kiện x > 0, ta có
logx + 2logx = log9 + logx
⇔ logx = log3 ⇔ x = 3
b) Với điều kiện x > 0, ta có
4logx + log4 + logx = 2log10 + 3logx
⇔ logx = log5 ⇔ x = 5
c) Ta có điều kiện của phương trình đã cho là:
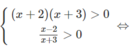
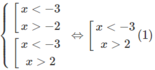
Khi đó, phương trình đã cho tương đương với:
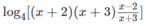
= log416 ⇔ x 2 − 4 = 16
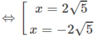
Cả hai nghiệm trên đều thỏa mãn điều kiện (1).
d) Với điều kiện x > 2, ta có phương trình
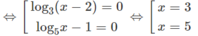
Cả hai giá trị này đều thỏa mãn điều kiện x > 2.
Đúng 0
Bình luận (0)
Giải các bất phương trình logarit sau:
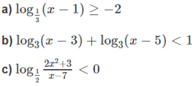
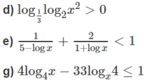
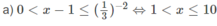
b)
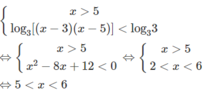
c)
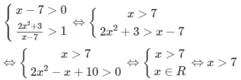
d)
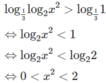
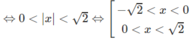
e) Đặt t = logx với điều kiện t ≠ 5, t ≠ −1 ta có:
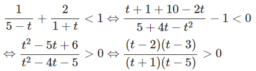
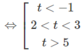
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy x < 1/10 hoặc 100 < x < 1000 hoặc x > 100 000.
g) Với điều kiện x > 0, x ≠ 1 đặt t = log 4 x
ta có: 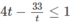
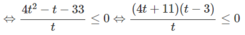
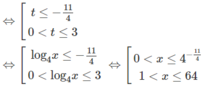
Đúng 0
Bình luận (0)
Giải các bất phương trình logarit sau: log 1 3 log 2 x 2 > 0
Giải các phương trình logarit sau: log x + log x 2 = log 9 x
Với điều kiện x > 0, ta có
log x + 2 log x = log9 + log x
⇔ logx = log3 ⇔ x = 3
Đúng 0
Bình luận (0)
Giải các phương trình logarit sau: log x 4 + log4x = 2 + log x 3
Với điều kiện x > 0, ta có
4logx + log4 + logx = 2log10 + 3logx
⇔ logx = log5 ⇔ x = 5
Đúng 0
Bình luận (0)
Giải các bất phương trình logarit sau: log 1 3 x - 1 ≥ - 2
Giải các bất phương trình logarit sau: 4 log 4 x - 33 log x 4 ≤ 1
Với điều kiện x > 0, x ≠ 1 đặt t = log 4 x
ta có: ![]()
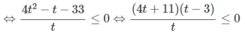
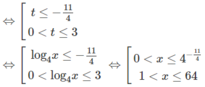
Đúng 0
Bình luận (0)
Giải các phương trình logarit sau: log 3 x - 2 log 5 2 = 2 log 3 x - 2
Với điều kiện x > 2, ta có phương trình
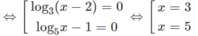
Cả hai giá trị này đều thỏa mãn điều kiện x > 2
Đúng 0
Bình luận (0)
Giải các bất phương trình logarit sau: log 1 2 2 x 2 + 3 x - 7 < 0