Tính diện tich các hình phẳng giới hạn bởi các đường sau:
Những câu hỏi liên quan
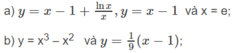
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = x 3 – 12x, y = x 2
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = 1 1 + x 2 , y = 1 2
π /2 - 1
Hướng dẫn:
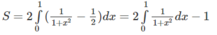
Đặt x = tan t để tính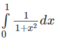 
Đúng 0
Bình luận (0)
Tính diện tích các hình phẳng giới hạn bởi các đường sau: y = x 3 - x 2 và y = 1 9 (x - 1)
8/81.
Hướng dẫn: Đường thẳng y = (x − 1)/9 đi qua tâm đối xứng 
của hàm số y =
x
3
-
x
2
.
Do đó, hình phẳng giới hạn bởi hai đường đã cho gồm hai hình vẽ đối xứng nhau qua điểm I (hình 85).
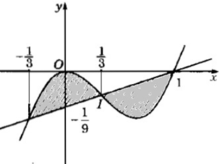
Vậy:
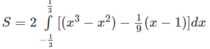
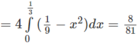
(theo bài 3.14.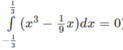 
)
Đúng 0
Bình luận (0)
Tính diện tích hình phẳng giới hạn bởi các đường sau: y xsin2x, y 2x,
x
π
2
A.
π
2
4
-
4
B.
π
2
-
π
C.
π
2
4
-
π...
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = xsin2x, y = 2x, x = π 2
A. π 2 4 - 4
B. π 2 - π
C. π 2 4 - π 4
D. π 2 4 + π 4
/
Chọn C.
Phương trình hoành độ giao điểm: x sin 2x = 2x <=> x (sin2x-2) = 0 <=> x = 0 hoặc sin2x = 2 (VN)
Đúng 0
Bình luận (0)
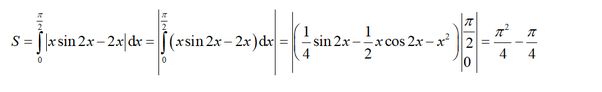
Tính diện tích hình phẳng giới hạn bởi các đường sau: y = 2x – x 2 , x + y = 2
Tính diện tích các hình phẳng giới hạn bởi các đường sau: y = x - 1 + lnx x , y = x - 1 và x = e
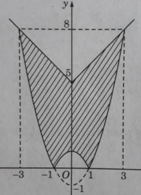
Tính diện tích của hình phẳng giới hạn bởi các đường sau: y = | x 2 – 1| và y = 5 + |x|
Hai hàm số y = | x 2 – 1| và y = 5 + |x| đều là hàm số chẵn. Miền cần tính diện tích được thể hiện ở Hình 8. Do tính đối xứng qua trục tung, ta có:
Đúng 0
Bình luận (0)
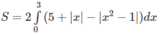
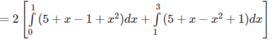
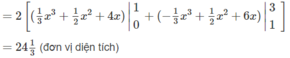
Tính diện tích hình phẳng D giới hạn bởi các đường 
A.1
B.2/3
C. 2
D. Đáp án khác
Tính diện tích hình phẳng D giới hạn bởi các đường :
A.10
B .11
C. 12
D.24
Ta có diện tích cần tính là:
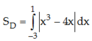
Mà 
nên ta có bảng xét dấu
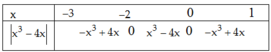
Do vậy
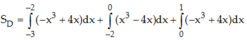
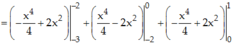
=12 (đvdt)
Chọn C
Đúng 0
Bình luận (0)