Giải phương trình: z - i 2 + 4 = 0 trên tập số phức.
(Đề thi tốt nghiệp THPT năm 2011)
Giải phương trình: ( z - i ) 2 + 4 = 0 trên tập số phức.
(Đề thi tốt nghiệp THPT năm 2011)
Giải phương trình sau trên tập số phức:
(1 – i)z + (2 – i) = 4 – 5i
(Đề thi tốt nghiệp THPT năm 2011)
(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
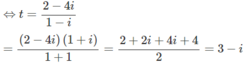
Giải phương trình sau trên tập số phức: (1 – i)z + (2 – i) = 4 – 5i (Đề thi tốt nghiệp THPT năm 2011)
(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
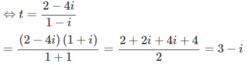
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
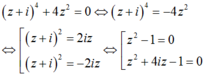
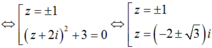
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Giải phương trình :
\(\left(z-i\right)^2+4=0\) trên tập số phức
đặc : \(z=a+bi\) với \(a;b\in R;i^2=-1\)
ta có : \(\left(z-i\right)^2+4=0\Leftrightarrow z^2-2iz+i^2+4=0\)
\(\Leftrightarrow\left(a+bi\right)^2-2i\left(a+bi\right)-1+4=0\)
\(\Leftrightarrow a^2+2abi+\left(bi\right)^2-2ai-2bi^2+3=0\)
\(\Leftrightarrow a^2+2abi-b^2-2ai+2b+3=0\)
\(\Leftrightarrow\left(a^2-b^2+2b+3\right)+\left(2ab-2a\right)i=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-b^2+2b+3=0\\2ab-2a=0\end{matrix}\right.\) \(\Leftrightarrow\left(a;b\right)\in\left\{\left(0;3\right)\left(0;-1\right)\left(2;1\right)\left(-2;1\right)\right\}\)
vậy \(z=3i;z=-i;z=2+i;z=-2+i\)
Giải các phương trình sau trên tập hơn số phức :
a) \(z^4+z^2-6=0\)
b) \(z^4+7z^2+10=0\)
a) Đặt Z = z2 , ta được phương trình Z2 + Z – 6 = 0
Phương trình này có hai nghiệm là Z1 = 2, Z2 = -3
Vậy phương trình có bốn nghiệm là ± √2 và ± i√3.
b) Đặt Z = z2 , ta được phương trình Z2 + 7Z + 10 = 0
Phương trình này có hai nghiệm là Z1 = -5, Z2 = -2
Vậy phương trình có bốn nghiệm là ± i√2 và ± i√5.
Giải các phương trình sau trên tập số phức:
(3 + 2i)z - (4 + 7i) = 2 - 5i
(3 + 2i).z - (4 + 7i) = 2 – 5i
⇔ (3 + 2i).z = (2 – 5i) + (4 + 7i)
⇔ (3 + 2i).z = 6 + 2i
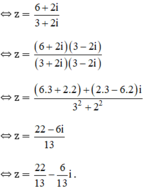
Cho phương trình trên tập họp số phức z 2 + a x + b = 0 . Nếu phương trình nhận số phức z = 1 + i làm một nghiệm thì a và b bằng.
A. a = -2, b = 2
B. a = 1, b = 5
C. a = 2, b = -2
D. a = 2, b = -4
Giải các phương trình sau trên tập số phức: 2 x 2 + 3x + 4 = 0