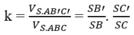Hình bên có số góc vuông là:
A. 6
B. 4
C. 8
Những câu hỏi liên quan
Khoanh vào chữ đặt trước câu trả lời đúng:
Trong hình bên có:
A. 4 góc vuông
B. 8 góc vuông
C. 12 góc vuông
D. 16 góc vuông
Số góc vuông trong hình bên là:
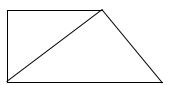
A. 5
B. 4
C. 3
D. 2
Đọc tiếp
Số góc vuông trong hình bên là:
A. 5
B. 4
C. 3
D. 2
6vr5h6cc f♥️🛴༼ つ ◕‿◕ ༽つ(っ.❛ ᴗ ❛.)っ(o´･_･)っ(o´･_･)っ(o´･_･)っ(o´･_･)っ(o´･_･)っ(つ✧ω✧)つ～(つˆДˆ)つ｡☆(っ.❛ ᴗ ❛.)っ(つ✧ω✧)つ(つ✧ω✧)つ(o´･_･)っ(つ≧▽≦)つ(o´･_･)っ༼ つ ◕‿◕ ༽つ(つ≧▽≦)つ(o´･_･)っ(o´･_･)っ(o´･_･)っ(o´･_･)っ(つ✧ω✧)つ🪔😍🎀💟😍
Xem thêm câu trả lời
Khoanh vào chữ đặt trước kết quả đúng:
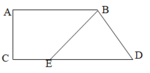
Số hình tam giác có trong hình bên là:
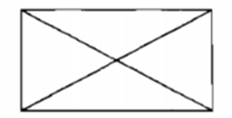
A. 4 B. 6
C. 7 D. 8
Phương pháp giải:
- Đếm các hình tam giác đơn.
- Ghép hình, đếm tiếp cho đến hết tất cả các hình tam giác.
Lời giải chi tiết:
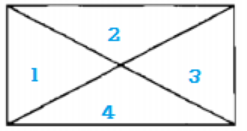
Hình trên có các hình tam giác là: 1; 2; 3; 4; 1+2; 2+3; 3+4; 4 +1.
Chọn đáp án D. 8.
Đúng 0
Bình luận (0)
Đúng ghi Đ, sai ghi S :
Trong hình bên :
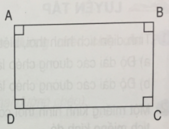
a) AB và DC là hai cạnh đối điện song song với nhau.
b) AB vuông góc với AD.
c) Hình tứ giác ABCD có 4 góc vuông.
d) Hình tứ giác ABCD có 4 cạnh bằng nhau.
a/đ b/đ c/đ d/s
Đúng ghi Đ, sai ghi S:Trong hình bên:a) AB và DC là hai cạnh đối điện song song với nhau.b) AB vuông góc với AD.c) Hình tứ giác ABCD có 4 góc vuông.d) Hình tứ giác ABCD có 4 cạnh bằng nhau.
Đọc tiếp
Đúng ghi Đ, sai ghi S:
Trong hình bên:
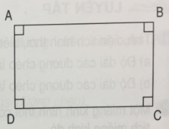
a) AB và DC là hai cạnh đối điện song song với nhau.
b) AB vuông góc với AD.
c) Hình tứ giác ABCD có 4 góc vuông.
d) Hình tứ giác ABCD có 4 cạnh bằng nhau.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B,
A
B
B
C
2
,
A
D
4
;
mặt bên SAD nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối S.BCD bằng A. 6 B. 18 C. 2 D. 1
Đọc tiếp
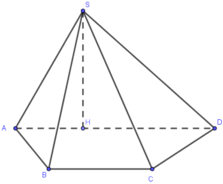
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, A B = B C = 2 , A D = 4 ; mặt bên SAD nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối S.BCD bằng
A. 6
B. 18
C. 2
D. 1
Đáp án C
Phương pháp:
Thể tích khối chóp: V = 1 3 S h
Cách giải:
Kẻ SH vuông góc AB (H thuộc AB). Do mặt bên SAD nằm trong mặt phẳng vuông góc với đáy ⇒ SH ⊥ (ABCD)
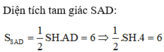
=> SH =3
Thể tích khối S.BCD
Đúng 0
Bình luận (0)
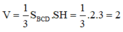
Điền số vào ô trống: Hình bên có:
a. ……..góc nhọn
b. ……..góc tù
c. ……..góc vuông
Hình bên có:
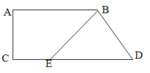
a…4…..góc nhọn
b …2..góc tù
c…2…..góc vuông
Đúng 0
Bình luận (0)
Hình bên có số đường thẳng vuông góc với AB là:
A. 7 đường thẳng B. 4 đường thẳng
C. 2 đường thẳng D. 5 đường thẳng
Ko có hình thì làm kiểu j :))
có thấy hình đâu phải có hình mới làm được chứ
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, SA vuông góc (ABCD). a) CM : BC vuông góc (SAB) và các mặt bên của hình chóp là các tam giác vuông. b) Gọi H,K là hình chiếu của A trên SB và SO. C/M : AH vuông góc SC va AK vuông góc BD c) C/M : K là trực tâm tam giác SBD
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
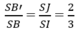
Do đó dễ thấy
Đúng 0
Bình luận (0)