Giải các hệ phương trình sau bằng máy tính bỏ túi.
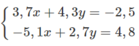
Giải các hệ phương trình sau bằng máy tính bỏ túi.
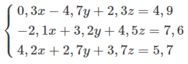
Giải các hệ phương trình sau bằng máy tính bỏ túi.
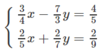
Giải các hệ phương trình sau bằng máy tính bỏ túi.
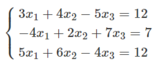
Giải phương trình sau bằng máy tính bỏ túi 3x2 + 4x + 1 = 0
3x2 + 4x + 1 = 0
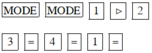
Màn hình hiện x1 = –0.3333333333
Ấn tiếp  , màn hình hiện x2 = –1.
, màn hình hiện x2 = –1.
Vậy nghiệm gần đúng của phương trình là: x1 = –0,33; x2 = –1
Giải phương trình sau bằng máy tính bỏ túi 5x2 - 3x - 7 = 0
5x2 – 3x – 7 = 0
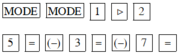
Màn hình hiện x1 = 1,520655562
Ấn tiếp  , màn hình hiện x2 = –0,9206555616
, màn hình hiện x2 = –0,9206555616
Vậy nghiệm gần đúng của phương trình là: x1 = 1,52; x2 = –0,92
Giải phương trình sau bằng máy tính bỏ túi 0,2x2 + 1,2x - 1 = 0
0,2x2 + 1,2x – 1 = 0
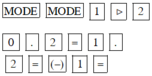
Màn hình hiện x1 = 0.7416573868
Ấn tiếp  , màn hình hiện x2 = –6.741657387
, màn hình hiện x2 = –6.741657387
Vậy nghiệm gần đúng của phương trình là: x1 = 0,74; x2 = –6,74
Giải phương trình sau bằng máy tính bỏ túi √2 x2 + 5x + √8 = 0
√2 x2 + 5x + √8 = 0
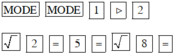
Màn hình hiện x1 = –0.7071067812
Ấn tiếp  , màn hình hiện x2 = –2.828427125
, màn hình hiện x2 = –2.828427125
Vậy nghiệm gần đúng của phương trình là: x1 = –0,71 ; x2 = –2,83
Giải các phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ ba)
a) 2x2 - 5x - 4 = 0 ; b) -3x2 + 4x + 2 = 0
c) 3x2 + 7x + 4 = 0 ; d) 9x2 - 6x - 4 = 0.
Giải các hệ phương trình sau bằng máy tính bỏ túi :
a) \(\left\{{}\begin{matrix}3x_1+4x_2-5x_3=12\\-4x_1+2x_2+7x_3=7\\5x_1+6x_2-4x_3=12\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}0,3x-4,7y+2,3z=4,9\\-2,1x+3,2y+4,5z=7,6\\4,2x-2,7y+3,7z=5,7\end{matrix}\right.\)
a, (\(x_1,x_2,x_3\))\(\approx\)(-2,52;3,2;-1,35)
b, (x,y,z)\(\approx\)(-0,29;-0,22;1,71)