Giải và biện luận các phương trình sau theo tham số m.
![]()
Giải và biện luận theo tham số m các phương trình sau:
![]()
Điều kiện của phương trình là x ≠ -1, ta có
![]()
⇒ (m - 2)x + 3 = (2m - 1)(x + 1)
⇒ (m + 1)x = 4 - 2m (1)
Với m = -1 phương trình (1) vô nghiệm nên phương trình đã cho cũng vô nghiệm.
Với m ≠ -1 phương tình (1) có nghiệm ![]()
Nghiệm này thỏa mãn điều kiện x ≠ -1 khi và chỉ khi 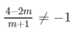 hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
Kết luận
Với m = -1 hoặc m = 5 phương trình vô nghiệm
Với m ≠ -1 và m ≠ 5 phương trình có nghiệm là ![]()
Giải và biện luận các phương trình sau theo tham số m.
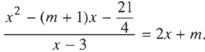
Điều kiện của phương trình là: x ≠ 3. Ta có:
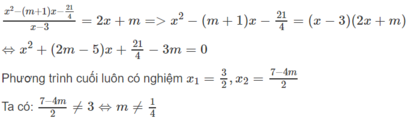
Kết luận
Với m ≠ 1/4 phương trình đã cho có hai nghiệm và x = 3/2 và x = (7 - 4m)/2
Với m ≠ 1/4 phương trình có một nghiệm x = 3/2
Giải và biện luận theo tham số m các phương trình sau:
![]()
Điều kiện của phương trình là x ≠ 1. Khi đó ta có
![]()
⇔ (2m + 1)x - m = (x + m)(x - 1)
⇔ x2 - (m + 2)x = 0
⇔ x = 0, x = m + 2
Giá trị x = m + 2 thỏa mãn điều kiện của phương trình khi m ≠ -1
Kết luận
Vậy với m = -1 phương trình có nghiệm duy nhất x = 0;
Với m ≠ -1 phương trình có hai nghiệm x = 0 và x = m + 2.
Giải và biện luận theo tham số m các phương trình sau:
![]()
Điều kiện của phương trình là x ≠ m . Khi đó ta có
![]()
⇔ (3m - 2)x - 5 = -3x + 3m
⇔ (3m + 1)x = 3m + 5
Với m ≠ -1/3 nghiệm của phương trình cuối là ![]()
Nghiệm này thỏa mãn điều kiện của phương trình khi và chỉ khi
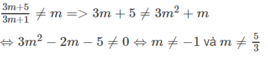
Kết luận
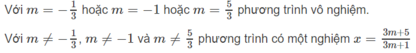
Giải và biện luận theo tham số m các phương trình sau:
![]()
Phương trình đã cho tương đương với phương trình
( m 2 - 6 m + 8 ) x = m 2 - m - 2
⇔ (m - 2)(m - 4)x = (m + 1)(m - 2)
Kết luận
Với x ≠ 2 và x ≠ 4 phương trình có nghiệm ![]()
Với m = 2, mọi số thực x đều là nghiệm của phương trình;
Với m = 4, phương trình vô nghiệm.
Giải và biện luận theo tham số m các phương trình sau
3 x + 2 m = x - m
Với ![]() phương trình đã cho trở thành
phương trình đã cho trở thành
3x + 2m = x - m ⇔ 2x = -3m ⇔ x = -3m / 2
Ta có:
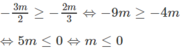
Với ![]() Phương trình đã cho trở thành
Phương trình đã cho trở thành
-3x - 2m = x - m ⇔ 4x = -m ⇔ x = -m / 4
Ta có:
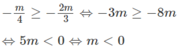
Kết luận
Với m > 0 phương trình vô nghiệm;
Với m = 0 phương trình có nghiệm x = 0;
Với m < 0 phương trình có nghiệm
![]()
Giải và biện luận các phương trình sau theo tham số m
m + 3 x 2 x - 1 = 3 x + 2
Điều kiện của phương trình là m ≠ 1/2. Khi đó ta có
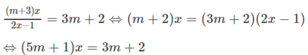
Nếu m ≠ -1/5 thì phương trình có nghiệm ![]()
Giá trị này là nghiệm của phương trình đã cho khi
![]()
Nếu m = -1/5 phương trình cuối vô nghiệm.
Kết luận.
Với m = -1/5 hoặc m = -3 phương trình đã cho vô nghiệm.
Với m ≠ -1/5 và m ≠ -3 nghiệm của phương trình đã cho là
![]()
Giải và biện luận theo tham số m các phương trình sau
4 x - 2 2 x - 1 = m - 1
Điều kiện của phương trình là m > 1/2
Với điều kiện đó vế trái dương, nên vế phải cũng dương nên m > 1. Lúc đó ta có:
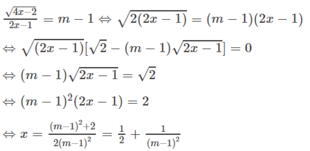
Giá trị ![]() thỏa mãn điều kiện x > 1/2
thỏa mãn điều kiện x > 1/2
Kết luận. Với m ≤ 1 phương trình vô nghiệm.
Với m > 1 nghiệm của phương trình là
![]()
Giải và biện luận theo tham số m các phương trình sau
2 x + m = x - 2 m + 2
![]()
Phương trình (1) ⇔ x = -3m + 2
Phương trình (2) ⇔ 3x = m - 2 ⇔ x = (m - 2) / 3
Vậy với mọi giá trị của m phương trình có nghiệm là:
x 1 = -3m + 2 và x 2 = (m - 2) / 3