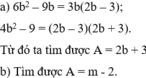Tìm số nguyên tố m,n thỏa mãn đẳng thức m2 - 6n2 = 1

Những câu hỏi liên quan
Tìm các số tự nhiên m,n và số nguyên tố p thỏa mãn mỗi đẳng thức sau:
a)p^m+p^n=p^m+n
b)p^m+p^n =p^m*n
Tìm các số nguyên tố x,y,z thỏa mãn đẳng thức :x^y+1=z
Ta thấy nếu x lẻ => VT chẵn => z chẵn ko phải số nguyên tố
Vậy x chỉ là số chẵn mà nguyên tố => x= 2
Với y=2 => z= 5 thỏa đk đề bài
Nếu y>2 => y lẻ (vì y nguyên tố)
=> y =2k +1
=> 2^(2k+1) +1 = 2.4^k + 1 = 2.(3p+1) + 1 = 3m
Như vậy khi x=2 và y nguyên tố > 2 thì VT luôn chia hết cho 3
=>z chia hết cho 3 không thỏa đk
Vậy x=y=2; z= 5 là duy nhất
Đúng 0
Bình luận (0)
bạn ơi ! Bạn please cho mình cách giải v~
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm các số tự nhiên m,n và số nguyên tố p thỏa mãn mỗi đẳng thức sau:
1)\(p^m+p^n=p^{m+n}\)
2)\(p^m+p^n=p^{m\times n}\)
Tìm các số tự nhiên m,n và số nguyên tố p thỏa mãn mỗi đẳng thức sau:
1)\(p^m+p^n=p^{m+n}\)
2)\(p^m+p^n=p^{m\times n}\)
Tìm ba số nguyên tố x,y,z thỏa mãn đẳng thức: xy+1=z
help
Ta thấy nếu x lẻ => VT chẵn => z chẵn ko phải số nguyên tố
Vậy x chỉ là số chẵn mà nguyên tố => x= 2
Với y=2 => z= 5 thỏa đk đề bài
Nếu y>2 => y lẻ (vì y nguyên tố)
=> y =2k +1
=> 2^(2k+1) +1 = 2.4^k + 1 = 2.(3p+1) + 1 = 3m
Như vậy khi x=2 và y nguyên tố > 2 thì VT luôn chia hết cho 3
=>z chia hết cho 3 không thỏa đk
Vậy x=y=2; z= 5 là duy nhất
Đúng 0
Bình luận (0)
Trả lời
Ta thấy nếu x lẻ => VT chẵn => z chẵn ko phải số nguyên tố
Vậy x chỉ là số chẵn mà nguyên tố => x= 2
Với y=2 => z= 5 thỏa đk đề bài
Nếu y>2 => y lẻ (vì y nguyên tố)
=> y =2k +1
=> 2^(2k+1) +1 = 2.4^k + 1 = 2.(3p+1) + 1 = 3m
Như vậy khi x=2 và y nguyên tố > 2 thì VT luôn chia hết cho 3
=>z chia hết cho 3 không thỏa đk
Vậy x=y=2; z= 5 là duy nhất
Với x=2; y=5 thì 2^5 + 1 =33 đâu phải số nguyên tố....
Đúng 0
Bình luận (0)
xy+1=zxy+1=z, ⇒z>2⇒z>2 ⇒z⇒z lẻ ⇒xy+1⇒xy+1 lẻ ⇒x⇒x chẵn ⇒x=2⇒x=2
Với y=2y=2: ⇒z=5⇒z=5 (thỏa mãn)
Với y>2y>2: 2y+1⋮2+1⇔z⋮32y+1⋮2+1⇔z⋮3 vì zz là số nguyên tố lớn hơn 33 mà z⋮3z⋮3 nên trường hợp này không tồn tại x,y,zx,y,z thỏa mãn đề bài (2y+1⋮2+12y+1⋮2+1 vì yy lẻ)
Vậy (x,y,z)(x,y,z)=(2,2,5)
Xem thêm câu trả lời
Tìm các số nguyên tố thỏa mãn đẳng thức sau : x2 - 2y2 = 1
Tìm tất cả các số nguyên tố (x;y) thỏa mãn đẳng thức: x2 - 2y2 = 1?
Biến đổi bt tương đương : (x^2-1) / 2 = y^2
Ta có: vì x,y là số nguyên dương nên
+) x > y và x phải là số lẽ.
Từ đó đặt x = 2k + 1 (k nguyên dương);
Biểu thức tương đương 2 * k * ( k + 1 ) = y ^ 2 (*);
Để ý rằng:
Y là 1 số nguyên tố nên y^2 sẽ là 1 số nguyên dương mà nó có duy nhất 3 ước là :
{1,y, y^2} ;
từ (*) dễ thấy y^2 chia hết cho 2, dĩ nhiên y^2 không thể là 2, vậy chỉ có thể y=2 =>k=1;
=>x=3.
Vậy ta chỉ tìm được 1 cặp số nguyên tố thoả mãn bài ra là x=3 và y=2 (thoả mãn).
Đúng 0
Bình luận (0)
Biến đổi bt tương đương : (x^2-1) / 2 = y^2
Ta có: vì x,y là số nguyên dương nên
+) x > y và x phải là số lẽ.
Từ đó đặt x = 2k + 1 (k nguyên dương);
Biểu thức tương đương 2 * k * ( k + 1 ) = y ^ 2 (*);
Để ý rằng:
Y là 1 số nguyên tố nên y^2 sẽ là 1 số nguyên dương mà nó có duy nhất 3 ước là :
{1,y, y^2} ;
từ (*) dễ thấy y^2 chia hết cho 2, dĩ nhiên y^2 không thể là 2, vậy chỉ có thể y=2 =>k=1;
=>x=3.
Vậy ta chỉ tìm được 1 cặp số nguyên tố thoả mãn bài ra là x=3 và y=2 (thoả mãn).
Nhớ like cho mình nha ^^
Đúng 0
Bình luận (0)
Tìm đa thức A thỏa mãn mỗi đẳng thức sau:a)
6
b
2
−
9
b
4
b
2
−
9
3
b
A
với
b
≠
±
3
2
;...
Đọc tiếp
Tìm đa thức A thỏa mãn mỗi đẳng thức sau:
a) 6 b 2 − 9 b 4 b 2 − 9 = 3 b A với b ≠ ± 3 2 ;
b) n − m 2 − m = m − n A với m ≠ 2 .
giả sử p và q là hai số nguyên tố thỏa mãn đẳng thức p(p-1)=q(q2-1) (*)
a) cmr tồn tại số nguyên k để p-1=kq; q2-1=kp
b) tìm tất cả các số nguyên tố p, q thỏa mãn pt (*)
ai làm đc thì trình bày nha :D