Gọi d là quỹ tích các điểm K ( 2m; 7m-1 ) là đường thẳng. Tìm hệ số góc của d

Những câu hỏi liên quan
Cho đường tròn (O), dây AB. Điểm C di chuyển trên AB và nằm ngoài đường tròn (O). Kẻ các tiếp tuyến CD, CE với đường tròn (D, E là các tiếp điểm). Tìm quỹ tích giao điểm K của OC và DE.
Cho 2 đường thẳng xx’ và yy’ vuông góc với nhau tại O. A là điểm cố định trên Ox, B là điểm cố định trên Oy mà OAOB. Gọi C là điểm chuyển động trên đoạn OB. Đường thẳng vuông góc với AC vẽ từ B cắt Ac tại E và xx’ tại Da)chứng minh OCOD.b) Tìm quỹ tích điểm Ec) Tìm quỹ tích điểm F là tâm đường tròn đi qua 4 điểm O,C,E,Dd)Chứng minh OE là phân giác của góc DEAe) Gọi G là hình chiếu của O xuống BD. Tìm quỹ tích của điểm G
Đọc tiếp
Cho 2 đường thẳng xx’ và yy’ vuông góc với nhau tại O. A là điểm cố định trên Ox, B là điểm cố định trên Oy mà OA=OB. Gọi C là điểm chuyển động trên đoạn OB. Đường thẳng vuông góc với AC vẽ từ B cắt Ac tại E và xx’ tại D
a)chứng minh OC=OD.
b) Tìm quỹ tích điểm E
c) Tìm quỹ tích điểm F là tâm đường tròn đi qua 4 điểm O,C,E,D
d)Chứng minh OE là phân giác của góc DEA
e) Gọi G là hình chiếu của O xuống BD. Tìm quỹ tích của điểm G
Cho ∆ABC vuông tại C, có BC =1/2AB. Trên cạnh BC lấy điểm E (E khác B và C). Từ B kẻ đường thẳng d vuông góc với AE, gọi giao điểm của d với AE, AC kéo dài lần lượt là I, K.
a. Gọi H là giao điểm của đường tròn đường kính AK với cạnh AB.
Chứng minh: H, E, K thẳng hàng.
b. Tìm quỹ tích điểm I khi E chạy trên BC.
Cho tam giác ABC có BC cố định và góc A bằng
50
°
. Gọi D là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm D A. Một cung chứa góc
115
°
dựng trên đoạn BC B. Một cung chứa góc
115
°
dựng trên đoạn AC C. Hai cung chứa góc
115
°
dựng trên đoạn AB D. Hai cung chứa góc
115
°
dựng trên đoạn BC
Đọc tiếp
Cho tam giác ABC có BC cố định và góc A bằng 50 ° . Gọi D là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm D
A. Một cung chứa góc 115 ° dựng trên đoạn BC
B. Một cung chứa góc 115 ° dựng trên đoạn AC
C. Hai cung chứa góc 115 ° dựng trên đoạn AB
D. Hai cung chứa góc 115 ° dựng trên đoạn BC
Chọn đáp án D
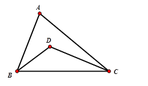
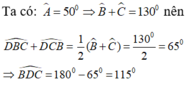
Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC cố định và góc A bằng
50
°
. Gọi D là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm D A. Một cung chứa góc
115
°
dựng trên đoạn BC B. Một cung chứa góc
115
°
dựng trên đoạn AC C. Hai cung chứa góc
115
°
dựng trên đoạn AB D. Hai cung chứa góc
115
°
dựng trên đoạn BC
Đọc tiếp
Cho tam giác ABC có BC cố định và góc A bằng 50 ° . Gọi D là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm D
A. Một cung chứa góc 115 ° dựng trên đoạn BC
B. Một cung chứa góc 115 ° dựng trên đoạn AC
C. Hai cung chứa góc 115 ° dựng trên đoạn AB
D. Hai cung chứa góc 115 ° dựng trên đoạn BC
Chọn đáp án D
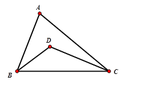
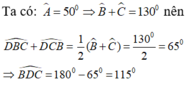
Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC
Đúng 0
Bình luận (0)
Bài 1 Cho tam giác ABC vuông tại A, BC cố địnha) Tìm quỹ tích điểm Ab) Gọi P là tđ AC. Tìm quỹ tích điểm P Nghe bảo quỹ tích của lớp 9Nhg cô mình dạy r:((Mn giúp mình với
Cho tam giác ABC có BC cố định và góc A bằng 50 0 . Gọi D là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm D
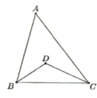
Ta có A ^ = 50 0 ⇒ B ^ + C ^ = 130 0
D B C ^ + D C B ^ = 65 0 ⇒ B D C ^ = 115 0
=> Quỹ tích của điểm D là hai cung chứa góc 115 0 dựng trên đoạn BC
Đúng 0
Bình luận (0)
Trong hình thoi ABCD người ta lấy các điểm P và Q theo thư tự tên AB và CD sao cho AP=1/3AB và CQ=1/3CD. Gọi I là giao điểm của PQ và AD,K là giao điểm của DP và BI,O là giao điểm của AC và BD
a) Cm AD=AI, cho biết nhận xét về tam giác BID và vị trí của K trên IB.
b) Cho B và D cố đình tìm quỹ tích A và I.
GIÚP MÌNH VỚI, MÌNH CẦN GẤP LẮM....😓
1: Cho tam giác ABC đều, đường cao AD, trực tâm H. M là điểm bất kỳ trên cạnh BC. Gọi E,
F thứ tự là hình chiếu của M trên AB và AC. Gọi I là trung điểm của AM. ID cắt EF tại K.
a) DEIF là hình gì?
b) CM: M, K, H thẳng hàng.
c) Xác định vị trí của M trên BC để EF đạt GTNN.
d) Tìm GTNN của SDEIF biết tam giác ABC có cạnh bằng a.
e) Tìm quỹ tích điểm K.
Giả sử M nằm giữa B and D
a)
tam giác IED có:
\(\hept{\begin{cases}IE=ID=\frac{1}{2}AM\\\widehat{EID}=2.\widehat{BAD}=60^0\end{cases}}\)
=> TAM GIÁC IED là tam giác đều (1)
Chứng minh tương tự ta được tam giác IFD là tam giác đều (2).
Từ (1) và (2) suy ra DEIF là hình thoi.
b) Vì
tam giác ABC đều nên trực tâm H củng là trọng tâm. Suy ra:
AH = 2.HD
Gọi P là trung điểm của AH
=> AP = PH = HD. Suy ra IP, KH thứ tự là đường trung bình của các tam giác AMH và DIP
=> MH // IP và KH // IP,
=> M , K , H thẳng hàng
c)
Vì tam giac EDK vuông tại K nên ta có: EF =2.EK = 2. ED.sinKDE =\(\sqrt{3}\).DE do đó EF đạt GTNN
=>DE đạt GTNN => \(DE\perp AB=>M\)trùng zs D ( Có thể dùng đ.lý pitago để tính EF theo DE ).
d) ta có diện tích DEIF=\(\frac{1}{2}DI.EF\)theo DE
e)e) Tìm quỹ tích của K thông qua quỹ tích của I.
bài này dài lắm . nên gợi ý như thế thôi . cần hỏi chỗ nào ib riêng cho mình ^^










