Cho tam giác ABC. Các điểm D, E di động trên các tia BA, CA sao cho 3BD=2CE. Chứng minh rằng tâm O của đường tròn ngoại tiếp tam giác ADE thuộc một đường thẳng cố định

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường cao AH và một điểm D di động trên đoạn AH. Trên các đoạn DB,DC lần lượt lấy E và F sao cho CE = CA, BF = BA. Chứng minh rằng tâm ngoại tiếp tam giác HEF luôn thuộc một đường cố định.
Gọi I là giao của BF và CE, đường tròn (HEF) cắt BC tại S khác H. Vẽ (B;BA) và (C;CA) cắt nhau tại M khác A
Kéo dài BD cắt (C) tại G khác E, CD cắt (B) tại K khác F. Dễ thấy A,H,M thẳng hàng nên ta có:
DF.DK = DA.DM = DE.DG do đó 4 điểm E,F,G,K đồng viên
Ta có BF2 = BA2 = BE.BG suy ra \(\Delta\)BEF ~ \(\Delta\)BFG (c.g.c). Tương tự \(\Delta\)CEF ~ \(\Delta\)CKE (c.g.c)
Từ đó ^BFE = ^BGF = ^CKE = ^CEF, suy ra \(\Delta\)EIF cân tại I
Gọi BF,CE cắt (HEF) lần lượt tại U,V. Dễ có SV // BE, SU // CF và FU = EV (Vì IE = IF)
Ta lại có \(BH.BS=BU.BF;CH.CS=CV.CE\Rightarrow\frac{BS}{CS}.\frac{BH}{CH}=\frac{BF}{CE}.\frac{BU}{CV}\)
Hay \(\frac{BS}{CS}.\frac{AB^2}{AC^2}=\frac{AB}{AC}.\frac{BU}{FU}.\frac{EV}{CV}=\frac{AB}{AC}.\frac{BS^2}{CS^2}\Rightarrow\frac{AB}{AC}=\frac{BS}{CS}\)
Suy ra S là chân đường phân giác trong kẻ từ đỉnh A của tam giác ABC
Vì vậy S cố định, khi đó đường tròn (HEF) đi qua hai điểm H,S cố định
Vậy thì tâm L của đường tròn (HEF) luôn thuộc trung trực của SH cố định (đpcm).
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A đường thẳng vuông góc với AB cắt nửa đường tròn trên tại I . K là một điểm bàng kỳ nằm trên đoạn thẳng CI ( K khác C và I ), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D.a, chứng minh : các tứ giác BCKM, ACMD nội tiếp đường tròn.b, chứng minh: ∆ABD~∆MBCc, chứng minh tâm đường tâm đường tròn ngoại tiếp tam giác ABC D nằm trên một đường thẳng tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố địn...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A đường thẳng vuông góc với AB cắt nửa đường tròn trên tại I . K là một điểm bàng kỳ nằm trên đoạn thẳng CI ( K khác C và I ), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D.
a, chứng minh : các tứ giác BCKM, ACMD nội tiếp đường tròn.
b, chứng minh: ∆ABD~∆MBC
c, chứng minh tâm đường tâm đường tròn ngoại tiếp tam giác ABC D nằm trên một đường thẳng tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định Khi K di động trên đoạn thẳn
Cho tam giác ABC ngoại tiếp đường tròn (O), (O) tiếp xúc với BC,CA,AB thứ tự tại D,E,F. Một điểm P di động trên đường tròn (O), gọi (PBF) cắt (PCE) tại K khác P. Chứng minh rằng đường thẳng đối xứng với PK qua phân giác của góc EPF đi qua điểm cố định.
Bổ đề: Xét tam giác ABC có X và Y thuộc BC sao cho AX và AY đối xứng nhau qua phân giác góc BAC thì \(\frac{XB}{XC}.\frac{YB}{YC}=\frac{AB^2}{AC^2}\).
Giải bài toán:
Gọi đường thẳng đối xứng với PK qua phân giác của ^EPF cắt EF tại S. Ta sẽ chỉ ra S cố định, thật vậy:
Kéo dài KP cắt EF tại L, PE cắt KC tại T, PF cắt KB tại G, KP cắt GT tại I
Ta có ^GKT = ^PKB + ^PKC = ^PFB + ^PEC = ^PEF + ^PFE = 1800 - ^GPT, suy ra tứ giác PTKG nội tiếp
Suy ra ^PGT = ^PKT = ^PEC = ^PFE do đó GT // FE. Từ đó, áp dụng Bổ đề, ta có biến đổi tỉ số:
\(\frac{LE}{LF}.\frac{SE}{SF}=\frac{PE^2}{PF^2}\Leftrightarrow\frac{SE}{SF}=\frac{PE^2}{PF^2}.\frac{LF}{LE}=\frac{PT^2}{PG^2}.\frac{IG}{IT}=\frac{PT^2}{PG^2}.\frac{IG}{IP}.\frac{IP}{IT}=\frac{PT^2}{PG^2}.\frac{KG}{PT}.\frac{PG}{KT}\)
\(=\frac{PT}{PG}.\frac{KG}{KT}=\frac{ET}{FG}.\frac{KG}{KT}=\frac{KP}{BF}.\frac{CE}{KP}=\frac{CE}{BF}\)
Hạ BN,CM vuông góc với EF, ta dễ có \(\frac{SE}{SF}=\frac{CE}{BF}=\frac{CD}{BD}=\frac{EM}{FN}=\frac{SE+EM}{SF+FN}=\frac{SM}{SN}\)
Chú ý rằng BN // CM và cùng vuông góc EF, do vậy DS vuông góc EF. Mà D,E,F cố định nên S cố định
Vậy ta thu được điều phải chứng minh.
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung
B
C
⏜
chứa A của (O). I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho
B
M
B
I
,
C
N
C
I
. Chứng m...
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung B C ⏜ chứa A của (O).
I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.
1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.
2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho B M = B I , C N = C I . Chứng minh rằng MN luôn đi qua một điểm cố định.
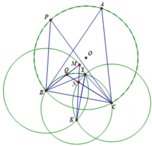
1) Ta có
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.
Đúng 0
Bình luận (0)
cho tam giác nhọn ABC nội tiếp đường tròn (O) . Các đường cao BD , CE ( D thuộc AC , E thuộc AB ) của tam giác kéo dài lần lượt cắt đường tròn (O) tại các điểm M và N ( M khác B , N khác C )1. CM tứ giác BCDE nộit tiếp được trong 1 đường tròn2. CM MN // DE3. khi đường tròn (O) và dây BC cố định , điểm A di động trên cung lớn BC sao cho tam giác ABC nhọn , cm bán kính đường tròn ngoại tiếp tam giác ADE không đổi và tìm vị trí của điểm A để S tam giác ADE đạt max
Đọc tiếp
cho tam giác nhọn ABC nội tiếp đường tròn (O) . Các đường cao BD , CE ( D thuộc AC , E thuộc AB ) của tam giác kéo dài lần lượt cắt đường tròn (O) tại các điểm M và N ( M khác B , N khác C )
1. CM tứ giác BCDE nộit tiếp được trong 1 đường tròn
2. CM MN // DE
3. khi đường tròn (O) và dây BC cố định , điểm A di động trên cung lớn BC sao cho tam giác ABC nhọn , cm bán kính đường tròn ngoại tiếp tam giác ADE không đổi và tìm vị trí của điểm A để S tam giác ADE đạt max
1. Do BD , CE là đường cao của tam giác ABC nên \(\widehat{BDC}=90^o\)và \(\widehat{BEC}=90^o\)
Vì E , D nằm cùng 1 phía trên nửa mặt phẳng có bờ là đường thẳng BC nên tứ giác BCDE nội tiếp trong đường trong đường kính BC
2. Trên cung tròn đường kính BC ta có : \(\widehat{D_1}=\widehat{C_1}\)( cùng chắc cung \(\widebat{BE}\))
Trên đường tròn (O) , ta có : \(\widehat{M_1}=\widehat{C_1}\)( cùng chắn cung \(\widebat{BN}\))
Suy ra : \(\widehat{D_1}=\widehat{M_1}\Rightarrow MN//DE\)( do có 2 góc đồng vị bằng nhau )
3. Gọi H là trực tâm của tam giác ABC và I là trung điểm của BC.
Xét tứ giác ADHE có \(\widehat{AEH}=90^o\)( do CE vuông AB )
\(\widehat{ADH}=90^o\)( do BD vuông AC )
\(\Rightarrow\widehat{AEH}+\widehat{ADH}=180^O\)nên tứ giác ADHE nội tiếp đường tròn đường kính AH
Vậy đường tròn ngoại tiếp tam giác ADE là đường tròn đường kính AH , có bán kính bằng \(\frac{AH}{2}\)
Kẻ đường kính AK của đường tròn (O) , ta có :
\(\widehat{KBA}=90^o\)( góc nội tiếp chắn nửa đường tròn (O) )
\(\Rightarrow KB\perp AB\)
mà \(CE\perp AB\left(gt\right)\)nên KB // CH (1)
Chứng minh tương tự ta có KC // BH (2)
Từ (1) và (2) => BKCH là hình bình hành
Vì I là trung điểm của BC suy ra I cũng là trung điểm của KH . Mặt khác ta có O là trung điểm của AK nên \(OI=\frac{AH}{2}\). Do BC cố định nên I cố định suy ra Oi không đổi
Vậy khi điểm A di động trên cung lớn BC thì độ dài bán kính đường tròn ngoại tiếp tam giác ADE luôn không đổi
Do tứ giác BCDE nội tiếp nên \(\widehat{ADE}=\widehat{ABC}\)( tính chất góc ngoài bằng góc trong đối diện ) (3)
Xét 2 tam giác ADE và ABC ta có \(\widehat{DAE}=\widehat{BAC}\), kết hợp với (3) ta có 2 tam giác này đồng dạng
\(\Rightarrow\frac{S_{\Delta ADE}}{S_{\Delta ABC}}=\left(\frac{AD}{AB}\right)^2=\left(\cos\widehat{DAB}\right)^2=\left(\cos\widehat{CAB}\right)^2\)
Do BC cố định nên cung nhỏ BC không đổi suy ra số đô góc CAB không đổi . Vậy để SADE đạt giá trị lớn nhất thì SABC cũng phải đạt giá trị lớn nhất . Điều này xảy ra khi và chỉ khi A là điểm chính giữa cung lớn BC
Bài 3. Cho tam giác ABC vuông ở A, với AC AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Đọc tiếp
Bài 3. Cho tam giác ABC vuông ở A, với AC > AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Cho tam giác ABC cân tại A, một điểm F di động trên cạnh AC và F không trùng với điểm A.
1) Xác định điểm E nằm trên đường thẳng AB sao cho trung điểm I của đoạn thẳng EF nằm trên cạnh BC.
2) Chứng minh rằng với điểm E xác định ở trên thì tâm đường tròn ngoại tiếp tam giác AEF nằm trên một đường thẳng cố định
giúp tôi câu c mọi người ơibài 1 cho tam giác ABC nhọn nội tiếp (O,R). hạ các đường cao AH và BK của tam giác. các tia AH và BK lần lượt cắt O tại điểm thứ hai là D và E.a. chứng minh tứ giác ABHK nội tiếp. tìm tâm của đường tròn đób.chứng minh rằng HK song song với DE.c. cho (O) và dây AB cố định, điểm C di động trên (O) sao cho tam giác ABC nhọn. CMR độ dài bán kính đương tròn ngoại tiếp tam giác CHK không đổi.
Đọc tiếp
giúp tôi câu c mọi người ơi
bài 1 cho tam giác ABC nhọn nội tiếp (O,R). hạ các đường cao AH và BK của tam giác. các tia AH và BK lần lượt cắt O tại điểm thứ hai là D và E.
a. chứng minh tứ giác ABHK nội tiếp. tìm tâm của đường tròn đó
b.chứng minh rằng HK song song với DE.
c. cho (O) và dây AB cố định, điểm C di động trên (O) sao cho tam giác ABC nhọn. CMR độ dài bán kính đương tròn ngoại tiếp tam giác CHK không đổi.
Cho đường tròn (O;R) và điểm A cố định với OA2R, BC là đường kính quay quanh O sao cho đường thẳng BC không đi qua A. Đường tròn ngoại tiếp tam giác ABC cắt AO tại I khác A. Các đường thẳng AB,AC cắt (O) lần lượt tại D và E. K là giao điểm của DE và AOa/ chứng minh bốn điểm K,E,C,I cùng thuộc một đường trònb/ tính độ dài đoạn AI theo Rc/ chứng minh rằng đường tròn ngoại tiếp tam giác ADE luôn đi qua 1 điểm cố định khác A khi đường kính BC quay quanh (O)
Đọc tiếp
Cho đường tròn (O;R) và điểm A cố định với OA=2R, BC là đường kính quay quanh O sao cho đường thẳng BC không đi qua A. Đường tròn ngoại tiếp tam giác ABC cắt AO tại I khác A. Các đường thẳng AB,AC cắt (O) lần lượt tại D và E. K là giao điểm của DE và AO
a/ chứng minh bốn điểm K,E,C,I cùng thuộc một đường tròn
b/ tính độ dài đoạn AI theo R
c/ chứng minh rằng đường tròn ngoại tiếp tam giác ADE luôn đi qua 1 điểm cố định khác A khi đường kính BC quay quanh (O)














