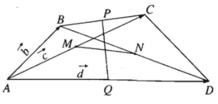
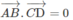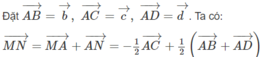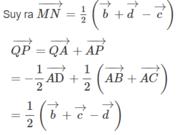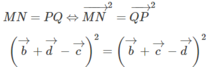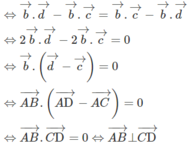Cho tứ diện ABCD. M,N lần lượt là trung điểm của AC và AD. Chứng minh AB⊥MN

Những câu hỏi liên quan
cho tứ giác abcd có m n p q lần lượt là trung điểm của ad ab bc cd.
chứng minh mn//ac và mn = 1 phần 2 ac
,chứng minh rằng mn=pq và mn//pq
Cho tứ diện ABCD. Hai điểm M, N lần lượt là trung điểm của AC, AD. Mặt phẳng (∝) chứa MN và song song với AB. Thiết diện của (∝) với tứ diện ABCD là:
A. hình thang
B. hình bình hành
C. hình chữ nhật
D. hình vuông
Đáp án B
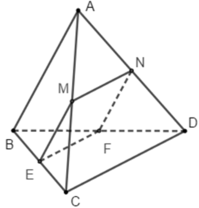
Mặt phẳng α chứa MN song song với AB
Gọi E và F lần lượt là trung điểm của BC và BD
Tam giác ABC có EM là đường trung bình nên ME // = 1/2 AB
Tam giác ABD có FN là đường trung bình nên FN // = 1/2 AB
Suy ra ME // FN // AB và ME = FN
Hay mặt phẳng (MNFE) chính là mặt phẳng α
Vậy thiết diện của mặt phẳng α với tứ diện là hình bình hành MNFE (do ME // = FN)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh MN ⊥ AB và MN ⊥ CD. Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
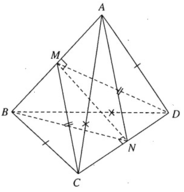
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD.
Bài 1 cho tứ giác ABCD, P,Q lần lượt là trung điểm của AD và BC,a chứng minh PQ hoặc AB AC 2,b tứ giác ABCD là hình thang PQ AB CD 2. Bài 2 cho hình thang ABCD, AB đáy lớn. M ,N,P,Q lần lượt là trung điểm của AD BC AC BD.a chứng Minh M N P Q thẳng hàng.b Cho AB a CD b với a b. Tính MN PQ.c Cm rằng nếu MP PQ QN thì a 2b
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm của cạnh BC và AD. Chứng minh rằng: MN ⊥ BC và MN ⊥ AD (h.3.42)
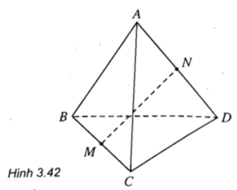
Tứ diện đều ABCD nên các mặt của tứ diện là các tam giác đều bằng nhau
Ta có: ∆BAD = ∆CAD (c.c.c)
Suy ra hai đường trung tuyến tương ứng bằng nhau: BN = CN
⇒ ΔBNC cân tại N.
Do NM là đường trung tuyến của tam giác cân BNC nên NM đồng thời là đường cao:
⇒ MN ⊥ BC
Chứng minh tương tự MN ⊥ AD
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
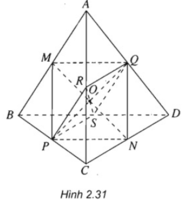
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt là trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MPNQ là hình bình hành. Từ đó suy ra 3 đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn ?
cho tứ giác abcd gọi m,n lần lượt là trung điểm của ab và dc, đường chéo ac cắt mn tại trung điểm i của mn, chứng minh diện tích tam giác abc bằng diện tích tam giác adc