Giải phương trình
a) x2 +2x +y2 -6y + 9= 0
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Cho đường tròn (C): x2+ y2 + 2x – 6y + 5= 0.Phương trình tiếp tuyến của (C) song song với đường thẳng (a) :
x+ 2y -15 = 0 là
A.x+ 2y= 0 và x+ 2y- 10= 0
B. x+ 2y= 2 và x+ 2y+ 8= 0
C. x+ 2y + 2= 0 và x+ 2y -8 = 0
D. tất cả sai
Đường tròn (C) có tâm I( -1;3) và bán kính. R = 1 + 9 - 5 = 5
Do tiếp tuyến d song song với đường thẳng a nên d có dạng: x + 2y - m = 0
d là tiếp tuyến của (C) khi và chỉ khi:
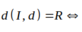
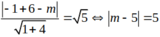
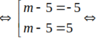
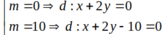
Chọn A.
Số nghiệm của hệ phương trình x 4 - 4 x 2 + y 2 - 6 y + 9 = 0 x 2 y + x 2 + 2 y - 22 = 0 là:
A. 4
B. 1
C. 2
D. 3
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x 2 + y 2 + 2 x - 6 y + 6 = 0 ; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình:
A. x 2 + y 2 - 6 x - 2 y + 6 = 0
B. x 2 + y 2 - 2 x - 6 y + 6 = 0
C. x 2 + y 2 + 6 x - 2 y - 6 = 0
D. x 2 + y 2 - 6 x + 2 y + 6 = 0
Phép đối xứng tâm I(1; 2) biến M(x; y) thành M’(x’; y’) thì:
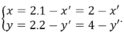
Thay vào phương trình (C) ta được:
2 - x ' 2 + 4 - y ' 2 + 2 ( 2 - x ' ) - 6 ( 4 - y ' ) + 6 = 0
⇒ x ' 2 + y ' 2 - 6 x ' - 2 y ' + 6 = 0 hay x 2 + y 2 - 6 x - 2 y + 6 = 0
Đáp án A
Phương trình nào sau đây là phương trình của đường tròn?
(I) x2+ y2 – 4x +15y -12= 0.
(II) x2+ y2 – 3x +4y +20= 0.
(III) 2x2+ 2y2- 4x + 6y +1= 0 .
A. Chỉ (I).
B. Chỉ (II).
C. Chỉ (III).
D. Chỉ (I) và (III).
Ta xét các phương án:
(I) có:
![]()
(II) có:
![]()
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
![]()
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 - 2 x - 4 y - 6 y - 11 = 0 . Tọa độ tâm T của (S) là
A. T(1;2;3)
B. T(2;4;6)
C. T(-2;-4;-6)
D. T(-1;-2;-3)
cho hệ phương trình \(\hept{\begin{cases}y^2-2x+3=0\\5x^2-7xy-6y^2=0\end{cases}}\)có 2 nghiệm (x1,y1); (x2,y2). tính x1+x2
Cho đường tròn (C) có phương trình x 2 + y 2 + 2 x − 6 y + 2 = 0 và điểm M(-2; 1). Đường thẳng ∆ qua M(-2; 1) cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB. Phương trình của ∆ là:
A.x + y + 1 = 0
B.x – y + 3 = 0
C.2x – y + 5 = 0
D.x + 2y = 0
ĐÁP ÁN D
Đường tròn (C) có tâm I( -1; 3).
Do đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB nên I M ⊥ Δ ( quan hệ vuông góc đường kính và dây cung).
Đường thẳng ∆: đi qua M(-2; 1) và nhận M I → ( 1 ; 2 ) làm VTPT nên có phương trình là :
1. (x + 2) + 2(y – 1) = 0 hay x+ 2y = 0
Trong không gian Oxyz, cho mặt cầu có phương trình x 2 + y 2 + z 2 + 2 x - 6 y - 6 = 0 . Tìm tọa độ tâm I và bán kính R của mặt cầu
A. I(1;-3;0), R=4
B. I(1;-3;0), R=16
C. I(-1;3;0), R=16
D. I(-1;3;0), R=4
Trong không gian Oxyz, cho mặt cầu có phương trình: x 2 + y 2 + z 2 + 2 x - 6 y - 6 = 0 . Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
A. I(1;-3;0), R=4
B. I(-1;3;0), R=4
C. I(-1;3;0), R=16
D. I(1;-3;0), R=16