Cho tứ giác ABCD, các điểm M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,CD,DA ; nối MN,NP,PQ,QM.Hãy chứng minh diện tích tứ giác MNPQ bằng 1/2 diện tích tứ giác ABCD

Những câu hỏi liên quan
Cho tứ giác ABCD. Các điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Nối MN, PQ, PQ, QM. Hãy chứng tỏ diện tích tứ giác MNPQ bằng ½ diện tích tứ giác ABCD.
Cho tứ giác ABCD. M,N,P,Q lần lượt là trung điểm các cạnh AB, CD, BC, DA. C/m: MP + NQ bé hơn hoặc bằng nửa chu vi của tứ giác
Cho tứ giác ABCD. M,N,P,Q lần lượt là trung điểm các cạnh AB, CD, BC, DA. C/m: MP + NQ bé hơn hoặc bằng nửa chu vi của tứ giác
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Vecto
M
N
→
không cùng phương với vecto nào? A.
P
Q
→
B.
A
P
→
C.
C
A
→
D.
Q
P...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Vecto M N → không cùng phương với vecto nào?
A. P Q →
B. A P →
C. C A →
D. Q P →
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN.
Suy ra, vecto M N → không cùng phương với vecto A P →
Đáp án B
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm các đường chéo của tứ giác MNPQ, trung điểm các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây đúng? A.
O
I
→
O
J
→
B.
O
A
→
...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm các đường chéo của tứ giác MNPQ, trung điểm các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây đúng?
A. O I → = O J →
B. O A → = O C →
C. O B → = O D →
D. O I → = - O J →
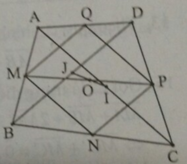
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D
Đúng 0
Bình luận (0)
Cho hình thang ABCD bốn điểm M N P Q lần lượt là trung điểm các cạnh AB BC CD DA biết diện tứ giác MNPQ là 115 cm2
*Ta có S 1= S QAM =1/2 S QAB(2 tam giác cùng chiều cao hạ từ đỉnh Q và đáy AM = 1/2 AB)
và S BQA =1/2 S BDA (2 tam giác cùng chiều cao hạ từ đỉnh B và đáy AQ = 1/2 AD)
=>S 1=1/4 S ABD
*Tương tự:
S 2 = 1/4 S ABC
S 3 = 1/4 S BCD
S 4 = 1/4 S ACD
=> S 1+ S 2+ S 3+ S 4 = 1/4 S (ABD + ABC + BCD + ACD) = 1/4 S (ABCD x 2) = 1/2 S ABCD
=> S MNPQ = S ABCD - 1/2 S ABCD = 1/2 S ABCD.
Vậy S MNPQ là : 115 : 2 = 57,5 ( cm2 )
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) CMR: Tứ giác MNPQ là hình bình hành
b) So sánh chu vi tứ giác MNPQ và tổng hai đường chéo của tứ giác ABCD.
Xem chi tiết
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA và I, K là trung điểm các đường chéo AC, BD. Chứng minh :
a) Các tứ giác MNPQ, INKQ là hình bình hành
Giúp mình với nhá, mai mình phải nộp bài rồi!!!
Đúng 0
Bình luận (0)
Cho hình thang ABCD. Bốn điểm M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Biết diện tích tứ giác MNPQ là . Diện tích hình thang ABCD là
230 nha nhớ tích cho mk đấy vì mk trả lời đầu tiên
Đúng 0
Bình luận (0)














