Cho hình thang ABCD có đáy AB ,CD .C/m BC=AD và BC // AD

Những câu hỏi liên quan
Cho hình thang ABCD có đáy AB và CD biết AB = CD . C/m BC=AD và BC//AD
CHo hình thang ABCD có đáy AB , CD . biết AB = CD . C/m BC =AD và BC // AD
Vì ABCD là hình thang có đáy AB,CD và AB=CD=>ABCD là hình thang=>BC=AD,BC//AD.
chúc bạn học tốt nhớ k cho mình nha!
Đúng 0
Bình luận (0)
Hình thang ABCD có AB=CD và AB//CD nên hình thang ABCD là hình bình hành.
=> \(BC=AD,BC//AD\)
Đúng 1
Bình luận (0)
cho hình thang ABCD có đáy AB và CD .C/m BC=AD và BC//AD
Cho hình thang ABCD có đáy AB,CD
A, Nếu AD//BC .CMR AD=BC và AB//BC
B,Nếu AB=CD .CMR AD//BC và AD=CD
hình thang ABCD có đáy AB, CD. cho AB=CD, CMR: AD//BC, AD=BC
Cho hình thang ABCD đáy AD và BC , AD+BC= AB . Gọi M là trung điểm CD
C/m Am vuông góc MB
Gọi E là giao điểm của AM với BC :
Xét tam giác ADM và tam giác ECM , ta có :
DM=CM (M là trung điểm của DC)
Góc M chung
Góc ADM =góc ECM (So le trong và AD//BC-gt)
Do đó:tam giác ADM = tam giác ECM (g.c.g)
Suy ra : AM=EM , AD=CE (cạnh tuong ứng)
AD+BC=AB (gt)
Mà AD=CE (cạnh tương ứng)
Nên BC+CE=AB
Suy ra BE=AB
Vậy tam giác ABE là tam giác cân tại B
Mà BM là đường trubg tuyến .Nên cũng là đường cao tam giác ABE.
Vậy BM vuông góc AM.
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD ( góc A = góc D = 90 độ ) . GỌI M ,N lần lượt là trung điểm cua BC , AD .
C/m : a) tam giác MAD cân
b ) góc MAB = goc MDC
Đúng 0
Bình luận (0)
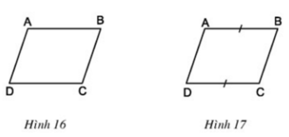
Hình thang ABCD có đáy AB, CD.
a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.
b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.
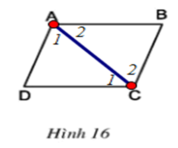
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
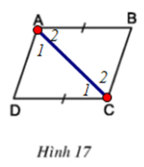
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
Đúng 2
Bình luận (0)
hình thang ABCD có đáy AB,CD
a) Cho biết AD//BC. Chứng minh AD=BC, AB=CD
b) Cho biết AB=Cd. Chứng minh AD//BC, AC=BC
tự vẽ hình
a) Xét tam giác DAC và tam giác BCA có:
góc DAC = góc BCA (slt do AD // BC)
AC: chung
góc DCA = góc BAC (slt do AB // DC)
suy ra: tam giác DAC = tam giác BCA (g.c.g)
=> AD = BC; DC = AB
b) Xét tam giác DAC và tam giác BCA có:
AD = AB
góc DCA = góc BAC (slt do AB // CD)
AC: chung
suy ra: tam giác DAC = tam giác BCA (c.g.c)
=> AD = BC
góc DAC = góc BCA
mà 2 góc này slt
=> AD // BC
Đúng 0
Bình luận (0)
Hình thang ABCD có đáy AB,CD
a)Cho biết AD//BC.Chứng minh AD=BC,AB=CD
b)Cho biết AB=CD.Chứng minh rằng AD//BC,AD=BC
a) Ta có : AB // CD ( do ABCD là hình thang )
AD // BC ( gt )
=> ABCD là hình bình hành
=> AD = BC ; AB = CD
b) Ta có : AB = CD ( gt )
AB // CD ( gt )
=> ABCD là hình bình hành
=> AD // BC ; AD = BC
Đúng 0
Bình luận (0)













