Giúp mk nha
Cho tam giác ABC vuông tại A,phân giác CD
H là hình chiếu của B lên đừng thẳng CD
Trên CD lấy điểm Esao cho H là trung điểm của DE
F là giao điểm của BH và CA
Cm:a, góc CBE=góc ADC
b, BE vuông góc BC
c, DF song song BE
Những câu hỏi liên quan
Bài 6: Cho tam giác ABC vuông tại A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là giao điểm của BH và CA. Chứng minh:
a) Góc CEB= góc ADC và Góc EBH= góc ACD
b) BE vuông góc BC
C) DF song song BE
Bài 5: Cho tam giác ABC vuông tại A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thắng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là giao điểm BH và CA. Chứng minh: a) CEB = ADC và EBH = ACD b) BE vuông góc với BC c) DF song song với BE
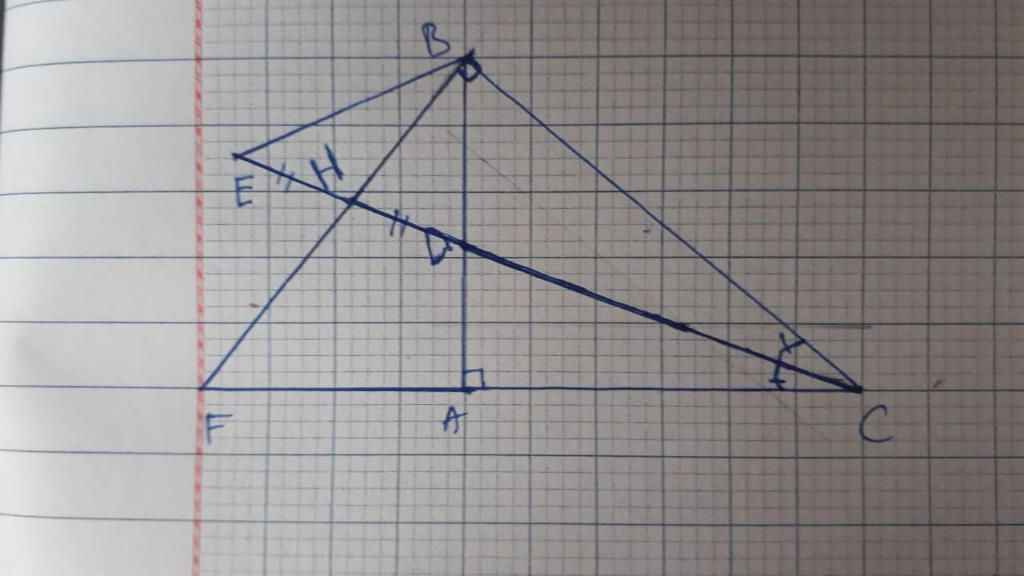
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là Giao điểm của BH và CA. Chứng minh rằng:
a) Góc CEB= góc ADC; góc EBH= góc ACD
b) BE vuông góc với BC
c) DF song song với BE
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là giao điểm của BH và CA. CMR:
a) góc CEB = góc ADC ; góc EBH = góc ACD
b) BE vuông góc với BC
c) DF song song với BE
các bạn ơi giúp mình với mình cảm ơn trước nha
a,\(\Delta\)BED có H là trung điểm của DE và BH \(\perp\) DE
=> \(\Delta\)BED cân ở B
=> Góc BED = Góc BDE
Góc BDE = Góc ADC (đối đỉnh)
=> Góc BED = Góc ADC
\(\Delta\)BED cân ở B => BH là phân giác của góc EBD
=> gócEHB = gócDBH
mà gócDBH = 90⁰ - gócBFA = 90⁰ - gócHFC = gócACD
=> gócEBH = gócACD
b, gócEBH = gócACD = gócDCB (vì CH là phân giác của gócACB)
= 90⁰ - gócCBH
=> gócEHB + gócCBH = 90⁰
=> BE \(\perp\) BC
c, △FBC có CH \(\perp\) BF ; BA \(\perp\) FC ; CH \(\cap\) BA = D
=> D là trực tâm của \(\Delta\)FBC
=> FD \(\perp\) BC
BE \(\perp\) BC
=> FD//BE
Đúng 0
Bình luận (3)
1) a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE
Đúng 0
Bình luận (0)
3) Cho tam giác ABC vuông ở A, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. Trên CD lấy điểm E sao cho H là trung điểm của DE. Gọi F là Giao điểm của BH và CA. Chứng minh rằng:
a) Góc CEB= góc ADC; góc EBH= góc ACD
b) BE vuông góc với BC
c) DF song song với BE
giúp mình với
Cho tam giác ABC, góc A = 90độ, phân giác CD. Gọi H là hình chiếu của điểm B trên đường thẳng CD. TreenCD lấy E sao cho H là trung điểm DE. Gọi F là giao diểm BH và CA. C/m
a) goác CEB = góc ADC Và góc EBH = ACD
b) BE vuông góc với BC
c) DF//BE
cho tam giác abc vuông tại a,đường phân giác cd(d thuộc ab).gọi h là hình chiếu của b trên đường thẳng cd.trên đường thẳng cd lấy e sao cho h là trung điểm đoạn thẳng ed.gọi f là giao điểm bh và ca
a)tam giác bhe=bhd và bf là tia phân giác góc ebd
b)góc fba=fch
c)eb//fd
( vẽ hình giùm mình nha~)
a, xét tam giác BHE và tam giác BHD có : BH chung
góc BHD = góc BHE = 90 do ...
HE = HD
=>tam giác BHE = tam giác BHD (2cgv)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A, đường phân giác CD (D thuộc AB). Gọi H là hình chiếu của B trên đường thẳng CD. Trên đường thẳng CD lấy điểm E sao cho H là trung điểm của đoạn thẳng ED. GỌi F là giao điểm của BH và CA.
a) Chứng minh tam giác BHE = tam giác BHD và BF là tia phân giác của góc EBD
b) Chứng minh góc FBA = góc FCH
c) Chứng minh EB // FD
Cho tam giác ABC vuông ở A,đường phân giác CD(D thuộc AB).Gọi H là hình chiếu của B trên đường thẳng CD.Trên đường thẳng CD lấy điểm E sao cho H là trung điểm của đoạn thẳng ED.Gọi F là giao điểm của BH và CA.
a,C/M tam giác BHE = tam giác BHD và BF là phân giác của góc EBD
b,C/M góc FBA=góc FCH
c,C/M EB//FD
a, Xét 2 t.giác vuông BHE và BHD có:
HD=HE(gt)
HB cạnh chung
=> t.giác BHE=t.giác BHD(cạnh góc vuông- cạnh góc vuong)
=> \(\widehat{EBH}\)=\(\widehat{DBH}\)(2 góc tương ứng)
=> BH là p/g của \(\widehat{EBD}\)<=>BF là p/g của \(\widehat{EBD}\)
Đúng 0
Bình luận (0)