so sánh tính chất giao hoán và kết hợp của phép nhân
tick cho 123 mỗi tuần
Hãy thực hiện các phép tính sau :
a, x y : y z
b, y z : x y
c, x y : y z : z x
d, x y : y z : z x
So sánh kết quả của a với kết quả của b; kết quả của c với kết quả của d
Phép chia có tính chất giao hoán và tính chất kết hợp hay không ?
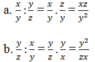
Kết quả câu b là nghịch đảo kết quả câu a.
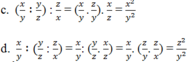
Kết quả câu c và d khác nhau. Phép chia không có tính chất giao hoán, tính chất kết hợp.
Cho ví dụ về tính chất giao hoán và tính chất kết hợp của phép cộng các số tự nhiên.
Cho ví dụ về tính chất giao hoán và kết hợp của phép nhân các số tự nhiên.
VD: - Tính chất giao hoán của phép cộng: 1 + 2 = 2 +1
- Tính chất kết hợp của phép cộng: 1 + 2 + 8 = 1 + (2+8)
- Tính chất giao hoán của phép nhân: 1.2 = 2.1
- Tính chất kết hợp của phép nhâ: 2.45.50 = (2.50).45
Căn cứ vào tính chất giao hoán và kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số.
Ví dụ. Tính chất giao hóa của phép nhân phân số:
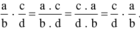
Bằng cách tương tự em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta có:
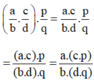
(áp dụng tính chất kết hợp của số nguyên cho cả tử và mẫu)
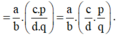
Vậy 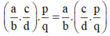 (tính chất kết hợp của phép nhân phân số)
(tính chất kết hợp của phép nhân phân số)
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân phân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp cua phép nhân phân số.
Ví dụ: Tính chất giao hoán của phép nhân phân số :
\(\frac{a}{b}.\frac{c}{d}=\frac{c.a}{d.b}=\frac{c}{d}.\frac{a}{b}\).
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên
(ab.cd).pq=a.cb.d.pq=(a.c).p(b.d).q(ab.cd).pq=a.cb.d.pq=(a.c).p(b.d).q
ab.(cd.pq)=ab.c.pd.q=a.(c.p)b.(d.q)ab.(cd.pq)=ab.c.pd.q=a.(c.p)b.(d.q)
Theo tính chất kết hợp của phép nhân các số nguyên ta có:
(a.c).p = a.(c.p) và b. (d.q) = (b. d) . q.
Do đó: (ab.cd).pq=ab.(cd.pq)
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân ps nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân ps
Vd: a/b×c/d=a×c/b×d=c×a/d×d=c/d×a/b
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân ps từ tính chất kết hợp của phép nhân số nguyên
Ai nhanh mk tk
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số
Ví dụ : Tính chất giao hoán của phép nhân phân số :
\(\dfrac{a}{b}.\dfrac{c}{d}=\dfrac{a.c}{b.d}=\dfrac{c.a}{d.b}=\dfrac{c}{d}.\dfrac{a}{b}\)
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên ?
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta suy ra tính chất kết hợp của phép nhân phân số:
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta suy ra tính chất kết hợp của phép nhân phân số:
nói và cho ví dụ về tính chất giao hoán và tính chất kết hợp của phép cộng các số tự nhiên .
Trong toán học, một phép tính R được coi là giao hoán nếu đổi thứ tự tính thì kết quả vẫn không thay đổi. Ví dụ: 34 + 45 = 45 + 34
a) tính chất giao hoán : 178230 - 26 + 178230 = 178230 - 178230 + 26
b) tính chất kết hợp : ( 1 + 2 ) +3 = 1 + ( 2 + 3)
Tính chất giao hoán: Khi đổi chỗ các số hạng trong 1 tổng thì tổng của chúng không thay đổi.
VD: a + b = b + a
Tính chất kết hợp: Muốn cộng tổng 2 số với số thứ 3, ta có thể cộng số thứ nhất với tổng của số thứ 2 và số thứ 3.
VD: ( a + b ) + c = a + ( b + c )
Tính chất giao hoán: Khi đổi chỗ các số hạng trong 1 tổng thì tổng của chúng không thay đổi.
VD: a + b = b + a
Tính chất kết hợp: Muốn cộng tổng 2 số với số thứ 3, ta có thể cộng số thứ nhất với tổng của số thứ 2 và số thứ 3.
VD: ( a + b ) + c = a + ( b + c )
Tính chất giao hoán: Khi đổi chỗ các số hạng trong 1 tổng thì tổng của chúng không thay đổi.
VD: a + b = b + a
Tính chất kết hợp: Muốn cộng tổng 2 số với số thứ 3, ta có thể cộng số thứ nhất với tổng của số thứ 2 và số thứ 3.
VD: ( a + b ) + c = a + ( b + c )
Viết dưới dạng tổng quát các tính chất giao hoán và kết hợp của phép cộng, phép nhân, tính chất phân phôíi của phép nhân đối với phép cộng
a+b=b+a
(a+b)+c=a+(b+c)=(a+c)+b
a.b=b.a
a(b+c)=ab+ac
tính nhanh bằng cách áp dụng tính chất giao hoán và kết hợp của phép nhân.Câu hỏi:25.7.10.4,4.36.25.50,32.125.3
Câu 1:
25.7.10.4
=(25.4)(7.10)
=100.70
=7000
Câu 2:
4.36.25.50
=(4.25)(18.2.50)
=100.1800
=180000
Câu 3:
32.2.125
=8.4.2.125
=(125.8)(4.2)
=1000.8
=8000
nhìn đầu bài khó luận quá bạn ạ!
bạn viết thưa ra rùi mình giải cho nhé!
câu 1: 25.7.10.4 câu 2: 4.36.25.50 câu 3: 32.125.3