CMR nếu tam giác ABC = tam giác A'B'C' thì những đường trung tuyến A'M' và AM của chúng cũng bằng nhau

Những câu hỏi liên quan
Gọi AM là trung tuyến của tam giác ABC, A'M là đường trung tuyến của tam giác A'B'C', Biết AM = A'M'; AB = A'B'; BC = B'C'. Chứng minh rằng hai tam giác ABC và A'B'C' bằng nhau
CM rằng nếu tam giác ABC = tam giác A'B'C' thì các trung tuyến AM, A'M' của chúng cũng bằng nhau. ( Vẽ hình hộ tớ nhá ^0^ )
Xem chi tiết
Cho AM = A'M' là trung tuyến của tam giác ABC và tam giác A'B'C' biết AM=A'M' , AB = A'B' , AC =A'C'
CMR: tam giác ABC và A'B'C'
a)cho tam giác A'B'C' đồng dạng tam giác ABC theo tỉ số k. Cho A'M', AM là trung tuyến. Chứng minh A'M'/AM= k
cho tam giác ABC bằng tam giác A'B'C', gọi M là trung điểm của BC, M' là trung điểm của B'C'. biết AM=A'M'. CMR:
a, tam giác AMB= tam giác A'M'B'
b,tam giác AMC= tam giác A'M'C'
Hai tam giác đó vẽ như này? True or False?
Đúng 0
Bình luận (0)
Cho tam giac ABC và tam giác A'B'C'. M là trung điểm của BC. M' là trung điểm của B'C'. Biết AB=A'B';AC=A'C'; AM=A'M'.CM tam giác ABC=tam giác A'B'C'
Cho tam giác ABC đồng dạng với tam giác ABC. Biết frac{AB}{AB}k. a) Viết các góc tương ứng bằng nhau và các tỷ số giữa các cạnh tương ứng b) Gọi AM và AM theo thứ tự lần lượt là trung tuyến của tam giác ABC và tam giác ABC. C/m: frac{BM}{BM}k.c) C/m: Tam giác ABM đồng dạng tam giác ABM. Suy ra tỷ số frac{AM}{AM}Các bạn giải nhanh câu c) giùm nha
Đọc tiếp
Cho tam giác ABC đồng dạng với tam giác A'B'C'. Biết \(\frac{AB}{A'B'}\)=k.
a) Viết các góc tương ứng bằng nhau và các tỷ số giữa các cạnh tương ứng
b) Gọi AM và A'M' theo thứ tự lần lượt là trung tuyến của tam giác ABC và tam giác A'B'C'. C/m: \(\frac{BM}{B'M'}\)=k.
c) C/m: Tam giác ABM đồng dạng tam giác A'B'M'. Suy ra tỷ số \(\frac{AM}{A'M'}\)
Các bạn giải nhanh câu c) giùm nha
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k, thì tỉ số của hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng k.
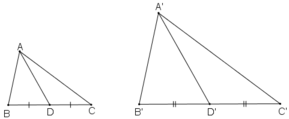
Giả sử ΔA’B’C’  ΔABC theo tỉ số k
ΔABC theo tỉ số k
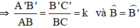
Gọi D, D’ lần lượt là trung điểm BC và B’C’
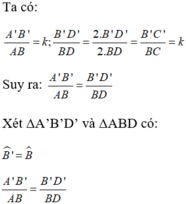
⇒ ΔA’B’D’ 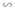 ΔABD theo tỉ số k.
ΔABD theo tỉ số k.
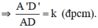
Đúng 0
Bình luận (0)
Cho tam giac ABC = tam giac A'B'C'.Gọi M là trung điểm của BC, M' là trung điểm của B'C'.Biết AM=A'M'.CMR :
a) tam giác ABC = tam giac A'B'C'
b) góc AMC= góc A'M'C'












