trên 1 đường thẳng lấy n điểm A1; A2; ........; An.Chia các điểm này vẽ các đường thẳng song song với nhau . Tính n để trong hình có 100 tia.
Mai mk cần rùi, cô giáo mà kiểm tra vào trúng mk mà ko lm là tèo lun, nên jup mk nha!!!!
Những câu hỏi liên quan
trên 1 đường thẳng lấy N điểm A1,A2,A3....AN qua các điểm này vẽ các đường thẳng song song với nhau .Tính giá trị của N để cho hình có 1000 tia
trên 1 đường thẳng lấy N điểm A1,A2,A3....AN qua các điểm này vẽ các đường thẳng song song với nhau .Tính giá trị của N để cho hình có 100 tia
Trên đường thẳng n lấy điểm A1,A2,A3,...,An.Chia các điểm này ra các đường thẳng song song với nhau.Tính n để trong hình có 100 tia
Trên một đường thẳng lấy n điểm A1, A2, A3…., An. Qua các điểm này vẽ các đường thẳng song song với nhau. Tính giá trị của n để trong hình có đúng 100 tia.
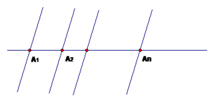
Tại mỗi điểm A1, A2,....,An đều có 4 tia.
Do đó để trong hình có 100 tia thì n = 100 : 4 = 25 (điểm)
Đúng 0
Bình luận (0)
15 tháng 8 2023 lúc 15:39
Cho đường thẳng xy và điểm O không thuộc xy. Lấy n điểm A1;A2;......An. Vẽ các tia gốc O lần lượt đi qua A1;A2;.....An. Biết trên hình có tất cả 40 tia. Tính giá trị của n
Xem chi tiết
15 tháng 8 2023 lúc 15:09
Cho đường thẳng xy và điểm O không thuộc xy. Lấy n điểm A1;A2;......An. Vẽ các tia gốc O lần lượt đi qua A1;A2;.....An. Biết trên hình có tất cả 40 tia. Tính giá trị của n
Xem chi tiết
15 tháng 8 2023 lúc 15:13
Cho đường thẳng xy và điểm O không thuộc xy. Lấy n điểm A1;A2;......An. Vẽ các tia gốc O lần lượt đi qua A1;A2;.....An. Biết trên hình có tất cả 40 tia. Tính giá trị của n
Xem chi tiết
Bổ sung giả thiết là \(n\) điểm đó nằm trên \(xy\)
Số các tia có gốc O là \(n\).
Ta nhận thấy số các tia có gốc là các điểm \(A_i\left(1\le i\le n\right)\) chính là \(A^2_n=\dfrac{n!}{\left(n-2\right)!}=n\left(n-1\right)=n^2-n\)
Từ đề bài, ta suy ra \(n^2-n+n=40\Leftrightarrow n^2=40\), vô lí.
(Mình nghĩ đề bài là 49 tia thì khi đó \(n=7\))
Đúng 2
Bình luận (0)
em ko biết cô hỏi xà lơ rách việc tự đi mà giải
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trên đường thẳng xy lấy 2018 điểm A1,A2,.........A2011,A2016. Và 1 điểm O nằm bên ngoài xy. Nối O với A1,A2,..A2016. Hỏi có bao nhiêu tam giác trên hình vẽ.
Trên đường thẳng xy lấy 2018 điểm A1,A2,.........A2011,A2016. Và 1 điểm O nằm bên ngoài xy. Nối O với A1,A2,..A2016. Hỏi có bao nhiêu tam giác trên hình vẽ.
Trên đường thẳng xy lấy 2018 điểm A1,A2,.........A2011,A2016. Và 1 điểm O nằm bên ngoài xy. Nối O với A1,A2,..A2016. Hỏi có bao nhiêu tam giác trên hình vẽ.