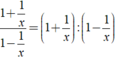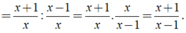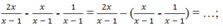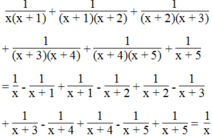1 x 1x 1x 1x1 x1 1x1x 1x 1 =

Những câu hỏi liên quan
tinh 1/3-1 x 1/5-1x1/7-1x.......x1/2017-1
G = (x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)(x+1x−1+xx+1+x1−x2):(x+1x−1+1−xx+1)
a) Rút gọn G b) Tìm giá trị nhỏ nhất của G với x > 0
c) Tính G tại | x - 3 | = 2 d) Tìm x với G = 1 ; G < 0
Biến đổi biểu thức
1
+
1
x
1
-
1
x
thành phân thức đại số là ? A.
x
+
1
x
-
1
B.
x
-
1...
Đọc tiếp
Biến đổi biểu thức 1 + 1 x 1 - 1 x thành phân thức đại số là ?
A. x + 1 x - 1
B. x - 1 x + 1
C. x x - 1
D. - x + 1 x - 1
Giải các phương trình sau:
1
-
x
-
1
x
+
1
(
x
+
2
)
x
+
1
x
-
1
+
x...
Đọc tiếp
Giải các phương trình sau: 1 - x - 1 x + 1 ( x + 2 ) = x + 1 x - 1 + x - 1 x + 1
ĐKXĐ: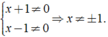
Ta có: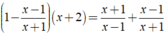
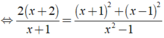
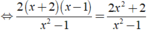
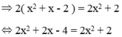
⇔ 2x = 6 ⇔ x = 3.
Vậy phương trình đã cho có nghiệm là x = 3.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
1
-
x
-
1
x
+
1
(
x
+
2
)
x
+
1
x
-
1
+
x...
Đọc tiếp
Giải các phương trình sau: 1 - x - 1 x + 1 ( x + 2 ) = x + 1 x - 1 + x - 1 x + 1
ĐKXĐ: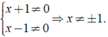
Ta có: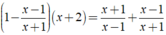
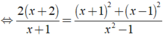
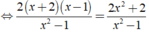
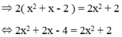
⇔ 2x = 6 ⇔ x = 3.
Vậy phương trình đã cho có nghiệm là x = 3.
Đúng 0
Bình luận (0)
Giải các phương trình:
x
+
1
x
-
1
-
x
-
1
x
+
1...
Đọc tiếp
Giải các phương trình: x + 1 x - 1 - x - 1 x + 1 1 + x + 1 x - 1 = x - 1 2 x + 1
Cách 1. ĐKXĐ: x ≠ ± 1. Biến đổi vế trái thành 4 x x 2 - 1 . x - 1 2 x = 2 x + 1
Ta đưa phương trình đã cho về dạng 2 x + 1 = x - 1 2 x + 1
Giải phương trình này bằng cách khử mẫu:
4(x + 1) = (x − 1)(x + 1)
⇔(x + 1)(x − 5) = 0
⇔x = −1 hoặc x = 5
Trong hai giá trị vừa tìm được, chỉ có x = 5 là thỏa mãn ĐKXĐ.
Vậy phương trình đã cho có một nghiệm duy nhất x = 5.
Cách 2. Đặt x + 1 x - 1 = y ta có phương trình y - 1 y 1 + y = 1 2 y
ĐKXĐ của phương trình này là y ≠ 0 và y ≠ −1. Giải phương trình này bằng cách khử mẫu:
2 y 2 − 2 = 1 + y
⇔2( y 2 − 1)−(y + 1) = 0
⇔(y + 1)(2y − 3) = 0
⇔y = −1 hoặc y = 3/2
Trong hai giá trị tìm được, chỉ có y = 3/2 là thỏa mãn ĐKXĐ
Vậy phương trình đã cho tương đương với phương trình x + 1 x - 1 = 3 2
Giải phương trình này ta được x = 5
Đúng 0
Bình luận (0)
Biến đổi mỗi biểu thức sau thành một phân thức đại số:
a) 1+1x1−1x1+1x1−1x; b) 1−2x+11−x2−2x2−11−2x+11−x2−2x2−1.
a) 1+1x1−1x1+1x1−1x =(1+1x):(1−1x)=x+1x:x−1x=x+1x.xx−1=x+1x−1=(1+1x):(1−1x)=x+1x:x−1x=x+1x.xx−1=x+1x−1
b) 1−2x+11−x2−2x2−11−2x+11−x2−2x2−1 =(1−2x+1):(1−x2−2x2−1)=(1−2x+1):(1−x2−2x2−1)
=x+1−2x+1:x2−1−(x2−2)x2−1=x+1−2x+1:x2−1−(x2−2)x2−1
=x−1x+1:x2−1−x2+2x2−1=x−1x+1:1(x−1)(x+1)=x−1x+1:x2−1−x2+2x2−1=x−1x+1:1(x−1)(x+1)
=x−1x+1.(x−1)(x+1)1=(x−1)2=x−1x+1.(x−1)(x+1)1=(x−1)2.
Đúng 0
Bình luận (0)
a) 1+1x1−1x1+1x1−1x =(1+1x):(1−1x)=x+1x:x−1x=x+1x.xx−1=x+1x−1=(1+1x):(1−1x)=x+1x:x−1x=x+1x.xx−1=x+1x−1 b) 1−2x+11−x2−2x2−11−2x+11−x2−2x2−1 =(1−2x+1):(1−x2−2x2−1)=(1−2x+1):(1−x2−2x2−1) =x+1−2x+1:x2−1−(x2−2)x2−1=x+1−2x+1:x2−1−(x2−2)x2−1 =x−1x+1:x2−1−x2+2x2−1=x−1x+1:1(x−1)(x+1)=x−1x+1:x2−1−x2+2x2−1=x−1x+1:1(x−1)(x+1) =x−1x+1.(x−1)(x+1)1=(x−1)2=x−1x+1.(x−1)(x+1)1=(x−1)2.
Đúng 0
Bình luận (0)
Thực hiện phép trừ
2
x
x
-
1
-
x
x
-
1
-
1
x
-
1
. Cách thực hiện nào sau đây là sai ?A.
2
x
x
-...
Đọc tiếp
Thực hiện phép trừ 2 x x - 1 - x x - 1 - 1 x - 1 . Cách thực hiện nào sau đây là sai ?
A. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - x x - 1 - 1 x - 1 = . . .
B. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - x x - 1 - 1 x - 1 = . . .
C. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - x x - 1 + 1 x - 1 = . . .
D. 2 x x - 1 - x x - 1 - 1 x - 1 = 2 x x - 1 - - x x - 1 + - 1 x - 1 = . . .
Chứng minh:
1
x
x
+
1
+
1
x
+
1
x
+
2
+
1
x
+
2...
Đọc tiếp
Chứng minh:
1 x x + 1 + 1 x + 1 x + 2 + 1 x + 2 x + 3 + 1 x + 3 x + 4 + 1 x + 4 x + 5 + 1 x + 5