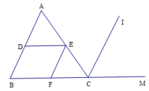
cho hình vẽ bên biết DE//BC,CI là tia phân giác của góc ACM; EF//CI. Chứng minh rằng EF là tia phân giác của góc DEC
Cho hình vẽ bên, biết DE // BC ; CI là tia phân giác của ACM ^ ; EF // CI . Chứng minh rằng EF là tia phân giác của DEC ^
Vì EF // CI nên MCI ^ = CFE ^ (hai góc đồng vị)
Vì DE // BC nên CFE ^ = DEF ^ (hai góc so le trong)
⇒ MCI ^ = DEF ^ (1)
Vì EF // CI nên FEC ^ = ACI ^ (hai góc so le trong) (2)
Mặt khác, ⇒ MCI ^ = ACI ^ (vì CI là tia phân giác của ACM ^ ) (3)
Từ (1), (2), (3) suy ra DEF ^ = FEC ^
Vậy EF là tia phân giác của DEC ^
a/
Ta có
DC=AD+BC (gt)
CI=BC (gt)
=> DC=AD+CI
Ta có
DC=DI+CI
=> AD=DI => tg ADI cân tại D \(\Rightarrow\widehat{DAI}=\widehat{DIA}\)
Mà \(\widehat{DAI}=\widehat{BAI}\)
\(\Rightarrow\widehat{DIA}=\widehat{BAI}\) Mà 2 góc này ở vị trí so le trong
=> AB//CD => ABCD là hình thang
b/
Ta có
CI=BC (gt) => tg BCI cân tại C \(\Rightarrow\widehat{CBI}=\widehat{CIB}\)
Ta có
AB//CD \(\Rightarrow\widehat{ABI}=\widehat{CIB}\) (góc so le trong)
\(\Rightarrow\widehat{CBI}=\widehat{ABI}\) => BI là phân giác của góc B
Cho tam giác ABC.Trên cạnh AB lấy điểm D,kẻ DE//BC (E thuộc AC).Vẽ tia phân giác Cx của góc ngoài tại đỉnh C.Từ E kẻ EF//CI (F thuộc BC).Chứng minh EF là tia phân giác của DEC
Cho tam giác ABC, gọi I là một điểm trên tia phân giác của góc ABC và điểm I nằm bên trong tam giác. Qua I kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại D và E biết DE= BD+CE. Chứng minh rằng CI là phân giác của góc ACB
Cho tam giác ABC. Lấy điểm D thuộc AB, E thuộc AC kẻ DE//BC. Gọi CM là tia đối của tia CB, Cy là tia phân giác của góc ACM. Kẻ EF//Cy. Chứng minh EF là tia phân giác của góc DEC
Cho tam giác ABC cân tại A . Trên tia đối của tia BA lấy D , trên tia đối của tia CA lấy điểm E sao cho BD = CE . Vẽ DM , CN vuông góc với BC .
a, Chứng minh ∆ ADE cân
b, Chứng minh DE // BC
c, Chứng minh ∆ AMN cân
d, Vẽ BH vuông góc với AM , CI vuông góc với AN . BH cắt CI ở K . Chứng minh AK là tia phân giác của góc MAN .
Bài làm
a) Ta có: AB + BD = AD
AC + CE = AE
Mà AB = AC, BD = CE ( gt )
=> AD = AE
=> Tam giác ADE cân tại A.
b) Vì tam giác ABC cân tại A
=> \(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\) (1)
Vì tam giác ADE cân tại A
=> \(\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\) (2)
Từ (1) và (2) => \(\widehat{ABC}=\widehat{ADE}\)
Mà hai góc này đồng vị.
=> BC // DE
c) Ta có: \(\widehat{ABC}=\widehat{MBD}\)( hai góc đối )
\(\widehat{ACB}=\widehat{NCE}\)( hai góc đối )
Mà \(\widehat{ABC}=\widehat{ACB}\)( Tam giác ABC cân )
=> \(\widehat{MBD}=\widehat{NCE}\)
Xét tam giác BMD và tam giác CNE có:
\(\widehat{BMD}=\widehat{CNE}=90^0\)
Cạnh huyền: BD = CE ( gt )
Góc nhọn: \(\widehat{MBD}=\widehat{NCE}\)( cmt )
=> Tam giác BMD = tam giác CNE ( cạnh huyền - góc nhọn )
=> BM = CN
Lại có: \(\widehat{ABC}+\widehat{ABM}=180^0;\widehat{ACB}+\widehat{ACN}=180^0\)
Mà \(\widehat{ABC}=\widehat{ACB}\)( Tam giác ABC cân )
=> \(\widehat{ABM}=\widehat{ACN}\)
Xét tam giác ABM và tam giác ACN có:
BM = CN ( cmt )
\(\widehat{ABM}=\widehat{ACN}\)( cmt )
AB = AC ( Do tam giác ABC cân tại A )
=> Tam giác ABM = tam giác ACN ( c.g.c )
=> AM = AN
=> Tam giác AMN cân tại A.
d) Chứng minh AH = IA nha, muộn r.
Xét tam giác AKH và tam giác AKI có:
\(\widehat{AHK}=\widehat{AIK}=90^0\)
Cạnh huyền: AK chung.
Cạnh góc vuông: AH = AI ( cmt )
=> Tam giác AKH = tam giác AKI ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{HAK}=\widehat{IAK}\)
=> AK phân giác của \(\widehat{HAI}\)
Hay AK là phân giác của \(\widehat{MAN}\)( đpcm )
a,Ta có ΔABCΔABC cân ở góc A => góc ABC=góc ACB =180(độ)−BAC2180(độ)−BAC2(1)
Ta có BD=CE(gt);AB=AC(gt)
mà AB+BD=AD và AC+CE=AE
=> AD=AE
=>ΔADEΔADE cân tại A ( Có hai góc bằng nhau)
=>góc ADE= góc AED=(180 độ - DAE) :2 (2)
Từ (1) và (2) => góc ABC= góc ADE=góc ACB=góc AED
mà góc ABC và góc ADE ở vị trí đồng vị
=>BC // DE(đpcm)
b)ta có góc ABC= góc MBD (đối đỉnh )
góc ACB= góc NCE( đối đỉnh )
mà Góc ABC=Góc ACB => góc MBD= góc NCE
Xét hai tam giác vuông ΔBMDΔBMD và ΔCNEΔCNE
có BD=CE (gt)
góc MBD= góc NCE (c/m trên)
=>ΔBMD=ΔCNEΔBMD=ΔCNE(Cạnh huyền - Góc nhọn)
=> DM=EN(Hai cạnh tương ứng)
c) Gọi giao điểm của AM và BI là E
giao điểm của AN và CI là F
Vì ΔBMD=ΔCNEΔBMD=ΔCNE( chứng minh trên ) =>BM=CN( Hai cạnh tương ứng)
Ta có : Góc ABC= Góc ACB ( gt)
mà Góc ABC + Góc ABM=180 độ ( kề bù)
và Góc ACB+góc ACN= 180 độ ( kề bù)
=>Góc ABM=góc ACN
Xét ΔABMΔABM VÀ ΔACNΔACN có:
AB=AC(gt)
Góc ABM=Góc ACN(cmt)
BM=CM ( cmt)
=> ΔABM=ΔACN(c−g−c)ΔABM=ΔACN(c−g−c)
=> Góc AMB=Góc ANC (hai góc tương ứng )
=> ΔAMNΔAMN Cân ở A ( có hai góc bằng nhau) (đpcm)
D,(hơi dài )
ta có tam giác AMN cân ở A=> AM=AN( hai cạnh bên) (3)
Xét hai tam giác vuông Tam giác EMB và tam giác FCN có:
Góc EMB=góc FNC (cmt)
MB=CN(cmt)
=> tam giác EMB= tam giác FNC ( cạnh huyền -góc nhọn)
=>EM=FN(hai cạnh tương ứng ) (4)
Ta có (3) (4) mà AE+EM=AM và AF+FN=AN
=> AE=AF
Xét hai tam giác vuông tam giác AEI và tam giác AFI có
AI cạnh chung
AE=AF(cmt)
=> tam giác AEI = Tam giác AFI (cạnh huyền-cạnh góc vuông)
=>Góc AIE=Góc AIF( góc tương ứng ) (10)
ta có góc EBM+MBD=góc EBD= góc ABI (đối đỉnh)(5)
góc FCN+NCE= Góc FCE= góc ACI( đối đỉnh )(6)
mà góc EBM= góc FCN (cmt)(7)
góc MDB=góc NCE(gt) (8)
từ (5)(6)(7)(8)=> góc ABI = góc ACI (9)
từ (9) (10)=> góc BAI=góc CAI ( tổng 3 góc của một tam giác ) (đpcm)
đề này thay ở câu d một tí nha , tuy tên gọi khác nhưng làm in hệt
d) Từ B và C kẻ các đường vuông góc với AN và AM, chúng cắt nhau tại I. Chứng minh rằng: AI là tia phân giác của góc BAC.
Cậu chép mạng đúng ko?
cho tứ giác ABCD có đường phân giác của góc A cắt DC ở I. biết CI = BC và DC = AD + BC . Chứng minh rằng : a. ABCD là hình thang . b. BI là tia phân giác của góc B
1, Cho tam giác ABC vuông cân tại A . Gọi M là trung điểm BC , D là đoạn thẳng BM ( D khác B và M ) . Kẻ các đường thẳng BH , CI lần lượt vuông góc với AD tai H và I . Cmr
a, góc BAM=góc ACM và BH và AI
b, Tam giác MHI vuông cân
c, Cho tam giác ABC có góc A =90 độ Kẻ AH vuông góc với BC (H thuộc BC ) . Tia phân giác của góc HAC cắt cạch BC ở điểm D và tia phân giác của góc HAB cắt cạch BC ở E . Chứng minh AB+AC = BC +DE