Cho 6 điểm phân biệt. Hãy vẽ 12 đường thẳng sao cho mỗi đường thẳng đi qua 2 điểm và giữa 2 đường thẳng không quá 2 điểm.

Những câu hỏi liên quan
Cho 9 điểm phân biệt, hãy kẻ 10 đường thẳng sao cho mỗi đường thẳng đi qua 3 điểm phân biệt
Ai làm và vẽ hình up lên mik sẽ tik cho
mình ko bt vẽ hình
Bài 1: Cho 4 điểm A,B,C,D phân biệt. Vẽ 2 đường thẳng đi qua 2 trong 4 điểm đã cho. Hỏi có thể vẽ được bao nhiêu đường thẳng?Bài 2:Cho 6 điểm A,B,C,D,E,F phân biệt. Hỏi có bao nhiêu đường thẳng đi qua 2 trong 6 điểm đã cho trong các trường hợp sau?a) Trong 6 điểm không có ba điểm nào thẳng hàng?b) Có 3 điểm thẳng hàng, có 4 điểm thẳng hàngBài 3: Cho n điểm phân biệt trong đó có đúng 7 điểm thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm trong n điểm đã cho. Có tất cả 190 đường thẳng. Tìm n?Mo...
Đọc tiếp
Bài 1: Cho 4 điểm A,B,C,D phân biệt. Vẽ 2 đường thẳng đi qua 2 trong 4 điểm đã cho. Hỏi có thể vẽ được bao nhiêu đường thẳng?
Bài 2:Cho 6 điểm A,B,C,D,E,F phân biệt. Hỏi có bao nhiêu đường thẳng đi qua 2 trong 6 điểm đã cho trong các trường hợp sau?
a) Trong 6 điểm không có ba điểm nào thẳng hàng?
b) Có 3 điểm thẳng hàng, có 4 điểm thẳng hàng
Bài 3: Cho n điểm phân biệt trong đó có đúng 7 điểm thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm trong n điểm đã cho. Có tất cả 190 đường thẳng. Tìm n=?
Mong mọi người giúp mình
Cho 3 điểm phân biệt A;B;C nằm trên đường thẳng d và điểm D không nằm trên da)Hỏi có bao nhiêu đường thẳng phân biệt đi qua ít nhất là 2 điểm trong 4 điểm A;B;C;D?Vẽ hình minh hoạ và kể tên các đường thẳng đób)Lấy thêm điểm E không nằm trên đường thẳng d và khác với điểm D.Hỏi bây giờ có bao nhiêu đường thẳng phân biệt,mỗi đường đi qua ít nhất là hai điểm trong 5 điểm A;B;C;D;E?
Đọc tiếp
Cho 3 điểm phân biệt A;B;C nằm trên đường thẳng d và điểm D không nằm trên d
a)Hỏi có bao nhiêu đường thẳng phân biệt đi qua ít nhất là 2 điểm trong 4 điểm A;B;C;D?Vẽ hình minh hoạ và kể tên các đường thẳng đó
b)Lấy thêm điểm E không nằm trên đường thẳng d và khác với điểm D.Hỏi bây giờ có bao nhiêu đường thẳng phân biệt,mỗi đường đi qua ít nhất là hai điểm trong 5 điểm A;B;C;D;E?
Trong các cách sau, có bao nhiêu cách để xác định một mặt phẳng 1. Đi qua 3 điểm phân biệt 2. Đi qua 1 điểm và chứa 1 đường thẳng không đi qua điểm đó 3. Đi qua 2 đường thẳng bất kì 4. Đi qua đường thẳng (d1) và song song với đường thẳng (d2) cho trước, sao cho d1 và d2 không cắt nhau 5. Song song với 2 đường thẳng cắt nhau 6. Song song với 2 đường thẳng chéo nhau 7. Đi qua 1 điểm và song song với một đường thẳng cho trước 8. Đi qua 1 điểm và song song với một m...
Đọc tiếp
Trong các cách sau, có bao nhiêu cách để xác định một mặt phẳng
1. Đi qua 3 điểm phân biệt
2. Đi qua 1 điểm và chứa 1 đường thẳng không đi qua điểm đó
3. Đi qua 2 đường thẳng bất kì
4. Đi qua đường thẳng (d1) và song song với đường thẳng (d2) cho trước, sao cho d1 và d2 không cắt nhau
5. Song song với 2 đường thẳng cắt nhau
6. Song song với 2 đường thẳng chéo nhau
7. Đi qua 1 điểm và song song với một đường thẳng cho trước
8. Đi qua 1 điểm và song song với một mặt phẳng cho trước
A. 2
B. 3
C. 4
D. 5
Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy
Đúng 0
Bình luận (0)
Vẽ hình theo các bước diễn đạt sau:- Vẽ năm điểm phân biệt A, B, C, D, E sao cho ba điểm A, B, C thẳng hàng; ba điểm B, C, D thẳng hàng; ba điểm B, C, E không thẳng hàng;- Vẽ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thảng phân biệt trong hình vẽ?- Vẽ đường thẳng a đi qua điểm e và song song với đường thẳng AB. Hỏi đường thẳng a có cắt đường thẳng CD không? Vì sao?
Đọc tiếp
Vẽ hình theo các bước diễn đạt sau:
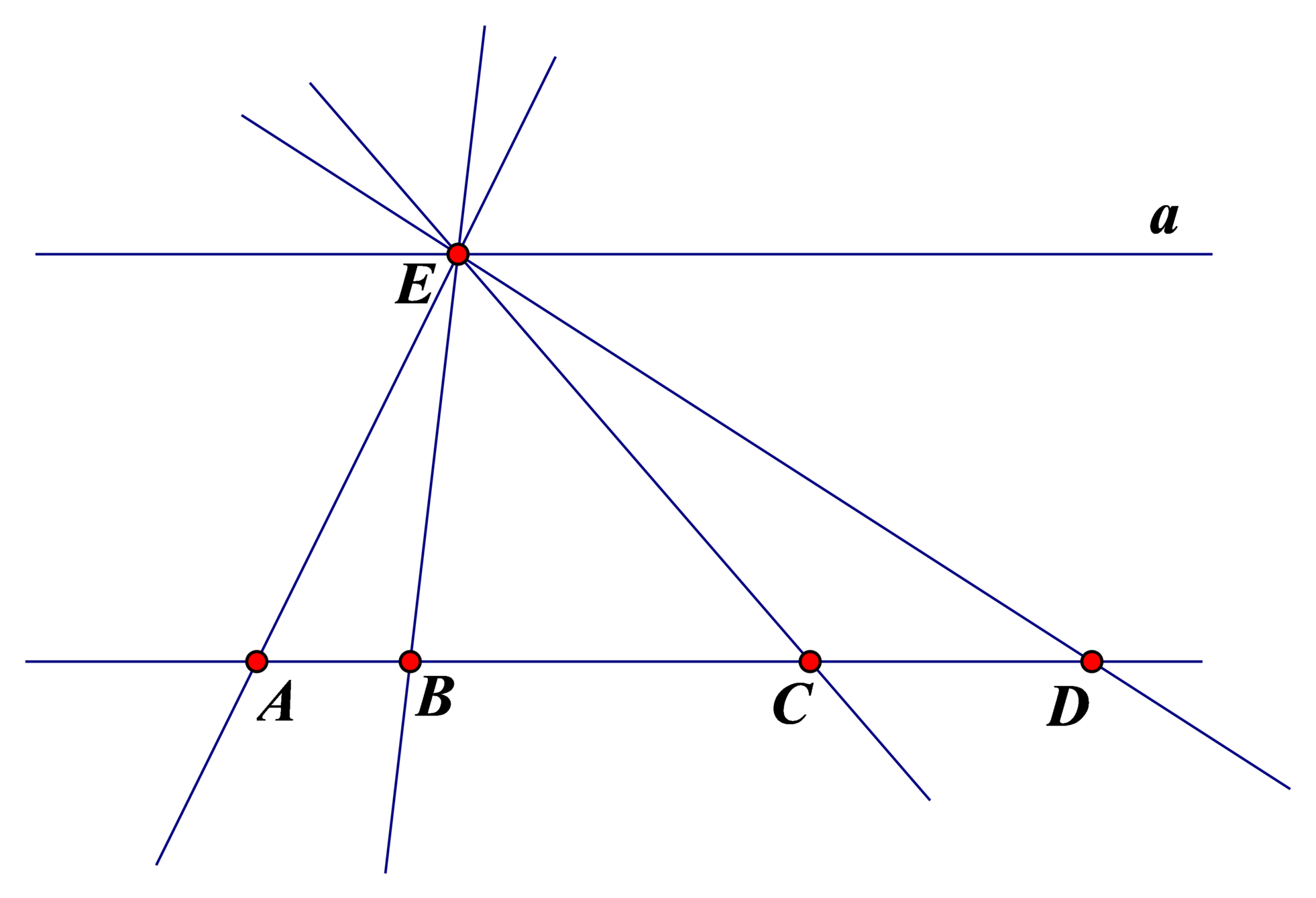
- Vẽ năm điểm phân biệt A, B, C, D, E sao cho ba điểm A, B, C thẳng hàng; ba điểm B, C, D thẳng hàng; ba điểm B, C, E không thẳng hàng;
- Vẽ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thảng phân biệt trong hình vẽ?
- Vẽ đường thẳng a đi qua điểm e và song song với đường thẳng AB. Hỏi đường thẳng a có cắt đường thẳng CD không? Vì sao?
- Có năm đường thảng phân biệt trong hình vẽ, đó là: EA , EB , EC , ED , AB .
- Hai đường thẳng AB và CD trùng nhau; đường thẳng a song song với đường thẳng AB nên cũng song song với đường thẳng CD. Do đó, đường thẳng a không cắt đường thẳng CD.
Đúng 0
Bình luận (0)
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
Đọc tiếp
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
câu này bó tay chấm com chấm vn vì mình mới có lớp 5
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
Đọc tiếp
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
+ Tổng số điểm phân biệt là: 4 + 5 + 6 + 7 + 1 = 23 điểm. Qua 2 điểm
vẽ được 1 đường thẳng nên ta có 23. 22 : 2 = 253 đường thẳng.
0,25
+ Mặt khác số các điểm thẳng hàng là 5;6;7;8 nên số các đường thẳng
trùng nhau là 10,15,21,28. Số đường thẳng cần tìm là: 253 - 10 - 15 -
0,25
21 - 28 + 4 = 183 đường thẳng
Trên 4 đường thẳng xx' ; yy' ; zz' và tt' có số điểm phân biệt tương ứng là 5, 6, 7, 8 => Số tia lần lượt tương ứng là 10, 12, 14, 16 => Tổng số tia cần tìm là 10 + 12 + 14 + 16 = 52 tia.
Tổng số điểm phân biệt là : 4 + 5 + 6 + 7 + 1 = 23 điểm. Qua 2 điểm ta vẽ được 1 đường thẳng nên ta có 23 . 22 : 2 = 253 đường thẳng.
Mặt khác số các điểm thẳng hàng là 5, 6, 7, 8 nên số các đường thẳng trùng nhau là 10, 15, 21, 28. Số đường thẳng cần tìm là : 253 - 10 - 15 - 21 - 28 + 4 = 183 đường thẳng.
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
Đọc tiếp
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
Cho 4 đường thẳng phân biệt xx ; yy ; zz và tt căt nhau tại O . Lấy 4 điểm , 5 điểm , 6 điểm , 7 điểm phân biệt khác O lần lượt thuộc bốn đường thẳng trên . Sao cho trong 3 điểm bất kì , mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng . Trên hình vẽ có bao nhiêu tia ? qua hai điểm vẽ được một đường thẳng , hỏi có thể vẽ được tất cả bao nhiêu đường thẳng ?
Đọc tiếp
Cho 4 đường thẳng phân biệt xx' ; yy' ; zz' và tt' căt nhau tại O . Lấy 4 điểm , 5 điểm , 6 điểm , 7 điểm phân biệt khác O lần lượt thuộc bốn đường thẳng trên . Sao cho trong 3 điểm bất kì , mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng . Trên hình vẽ có bao nhiêu tia ? qua hai điểm vẽ được một đường thẳng , hỏi có thể vẽ được tất cả bao nhiêu đường thẳng ?
có 52 tia
có 74 đường thẳng
mình làm vậy đó
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

















