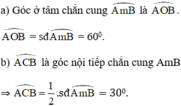Mỗi câu sau đây đúng hay sai
(A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó.
(B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
(C) Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau.
(D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn.
(E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
(A) Sai. Góc nội tiếp là góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung của đường tròn đó.
(B) Sai. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc chắn hai cung bằng nhau.
(C) Sai. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.
(D) Sai. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm cùng chắn một cung.
(E) Đúng. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Mỗi câu sau đây đúng hay sai ?
(A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó
(B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung
(C) Trong một đường tròn, hai góc nội tiếp khong cùng chắn một cung thì không bằng nhau
(D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo của cung bị chắn
(E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung
1. Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.
Câu 1 cho tứ giác ABCD nội tiếp nửa đường tròn kính AD. Hai đường chéo AC và BD cắt nhau tại d vẽ AD vuông góc với ad chứng minh A. Tứ giác ABEF nội tiếp B. AC là tia phân giác của góc BCF Câu 8 cho đường tròn tâm o đường kính AB. Vẽ dây cung CD vuông góc AB tại I (I nằm giữa a và o) lấy điểm e trên cung nhỏ BC (e khác b và c) AE cắt CD tại F. Chứng minh A. BEFI là tứ giác nội tiếp B. AE x AF = AC²
Trong hình 67, cung AmB có số đo là 60 ° . Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB
Cho tam giác ABC có 3 góc nhọn nội tiếp (O) đường cao BH và CK lần lượt cắt (O) tại E và F a)tứ giác BKHC nội tiếp b) OA vuông góc với EF c) EF song song HK d) Khi tam giác ABC là tam giác đều có cạnh bằng a tính diện tích hình viên phân chắn cung nhỏ BC của (O)
Cho tam giác ABC có 3 góc nhọn nội tiếp (O) đường cao BH và CK lần lượt cắt (O) tại E và F a)tứ giác BKHC nội tiếp b) OA vuông góc với EF c) EF song song HK d) Khi tam giác ABC là tam giác đều có cạnh bằng a tính diện tích hình viên phân chắn cung nhỏ BC của (O)
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc với AD ( F thuộc AD), CF cắt đường trong tại M. Chứng minh rằng:
a) các tứ giác ABEF;DCEF nội tiếp đường tròn.
B) tia CA là tia phân giác của góc BCF
C) BM vuông góc AD
Ta có: ˆACD=900ACD^=900 (góc nội tiếp chắn nửa đường tròn đường kính AD)
Xét tứ giác DCEF có:
ˆACD=900ACD^=900 (cm trên)
ˆEFD=900EFD^=900 (vì EF⊥ADEF⊥AD (gt))
⇒ˆACD+ˆEFD=1800⇒ACD^+EFD^=1800
=> Tứ giác DCEF là tứ giác nội tiếp đường tròn (đpcm).
b) Vì tứ giác DCEF là tứ giác nội tiếp (chứng minh câu a)
⇒ˆC1=ˆD1⇒C1^=D1^ (góc nội tiếp cùng chắn cung EF) (1)
Mà ⇒ˆC2=ˆD1⇒C2^=D1^ (góc nội tiếp cùng chắn cung AB) (2)
Từ (1) và (2) ⇒ˆC1=ˆC2⇒C1^=C2^
⇒⇒ CA là tia phân giác của ˆBCFBCF^ (đpcm)
k đúng hộ
cho tam giác ABC nội tiếp chắn nửa đường tròn,đường kính BC.Tiếp tuyến tại B của nửa đường tròn cắt AC tại D, lấy F thuộc cung AB, CF cát BD tại E, AF cắt BD tại K.
a) CM; góc ABD=AFC; tứ giác ADEF nội tiếp
b) tia phân giác của góc DCE cắt AF ở P và cắt BD ở M
Tia phân giác của góc AKD cắt CE ở Q và cắt CD ở N.
CM; tam giác KMP và tam giác CNQ là tam giác cân
c) CM; tứ giác MNPQ là tứ giác nội tiếp.
b)
+ Xét đt (o) có
tứ giác BFACN nội tiếp đt
\(\rightarrow ABC\)=AFC ( 2 góc nt cùng chắn cung AC)
CÓ :
BD là tiếp tuyến đt (o) tại B(gt)
\(\rightarrow\) BD vuông góc BO (TC tiếp tuyến)
\(\rightarrow\)BD vuông góc BC (O thuộc BC)
\(\rightarrow\) DBC = 90(dn)
\(\rightarrow\)tam giác DBC vuông tại B
xét tam giác vuông DBC cso
BDC+DCB=90(2 góc phụ nhau trong tg vuông) (1)
+Xét đt (o) có:
BAC= 90 ( góc nt chắn nửa dtđk BC)
\(\rightarrow\)tam giác BAC vuông tại A
Xét tam giác vuông BAC có
ABC+ACB=90 (2 gọc phụ nhau trong tam giác vuông)
\(\rightarrow\) ABC+DCB=90(A thuộc DC ) (2)
từ(1) và(2) \(\rightarrow\) BDC=ABC( cùng phụ DCB)
Mà AFC=ABC(CMT)
\(\rightarrow\) BDC=AFC(=ABC)
+Có :
AFC+AFE=180( 2 góc kề bù)
Mà 2 góc ở vị trí đối nhau
\(\rightarrow\) tứ giác DEFA nội tiếp ( DHNB tứ giác nội tiếp)
| |
Trên nữa đường tròn (O) đường kính AB lấy hai điểm C, D sao cho cung AC < cung AD, (C khác A; D khác B). Các đoạn thẳng AD, BC cắt nhau tại H. vẽ HE vuông góc với OA tại E (E nằm giữa hai điểm O và B). Chứng minh: OCDE là tứ giác nội tiếp
