a. Theo đề => x \(\in\)BC(24, 180)

Ta có: 24=2³.3; 180 = 2².3².5

=> BCNN(24, 180)=2³.3².5=360

=> x \(\in\)BC(24,180)=B(360)={0; 360; 720; 1080;...}

Mà 0 < x < 1000

Vậy x \(\in\){360; 720}.

b. +) Nếu n chẵn thì n=2k

Ta có: (n+4).(n+7) = (2k+4).(2k+7) = 2.(k+2).(2k+7) chia hết cho 2 nên là số chẵn.

+) Nếu n lẻ thì n=2k+1

Ta có: (n+4).(n+7) = (2k+1+4).(2k+1+7) = (2k+5).(2k+8) = (2k+5).2.(k+4) chia hết cho 2 nên là số chẵn.

Vậy...

vì 180,84 chia hết chõ nên x thuộc ƯC(180,84)

180=2^2x3^2x5

84=2^2x3x7
ƯCLN(180,84)=2^2x3=12

ƯC(180,84)=Ư(12)={2;3;4;6;12}

Vậy A={2;3;4;6;12}

6 thêm 1 nữa

Ta có:84 chia hết cho x

         180 chia hết cho x

=>x thuộc UC(84,180)

mà 84=2^2.3.7

180=2^2.3^2.5

=>UCLN(84,180)=12

=>UC(84,180)=1;2;3;4;6;12

Tập họp A có 6 phần tủ.

Ta co : 180,84 chia het cho x 

Gồm có 6 phần tử

Bạn chỉ cần tìm BCNN của 180;84

Ta có : 180,84 chia hết cho x

suy ra : x thuộc ước chung của 180 và 84

180=2^2.3^2.5

84=2^2.3.7

UWCLN(180,84)=2^2.3=12

suy ra x thuộc ước của 12

Ư (12)=1,2,3,4,6,12

vậy có 6 phần tử

là 6 mk lm đúng ở violympic rồi

Vì 180,84 chia hết cho nên x thuộc ƯC (180;84)

180 = 2^2 x 3^2 x 5

84 = 2^2 x 3 x7

WCLN (180;84) 2^2 X 3 = 12

ưc (180;84) = ư (12)

=[1;12;2;6;3;4]

Vậy A = [1;12;2;6;3;4]

ẤN Đúng đi

UCLN(84 ; 180) = 12

Ư(12) = {1;2;3;4;6;12}

Vậy có 6 số 

vì 180,84 chia hết cho x nên x thuộc ƯC(84;180)

180=2² x3² x5

84=2²x3x7

=> ƯCLN(84;180)=2²x3=12

=> ƯC(180;84)=Ư(12)={2;3;4;6;12}

Vậy A có 6 phần tử

a) X = {2012 ; 2016 ; 2020 ; 2024}

b)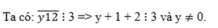

y + 3 ⋮ 3 => y ⋮ 3

Mà: y ∈ {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6} và y ≠ 0 nên y ∈ {3 ; 6}.

Vậy số cần tìm là 312 ; 612.

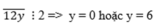
Vậy số cần tìm là 120 ; 126.