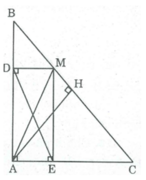
Bài 1: Cho tam giác ABC (góc A= 90o),M là điểm chuyển động trên BC. Vẽ MD vuông góc AB, ME vuông góc AC(D thuộc AB,E thuộc AC). Xácđịnh vị trí của M đễ đoạn thẳng DE có độ dài nhỏ nhất.
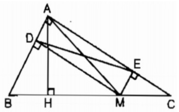
Bài 2:Cho tam giác ABC, từ A dựng đường thẳng d cắt cạnh AB. Xác định vị trí của d sao cho tổng khoảng cách từ B và C đến d nhỏ nhất, lớn nhất.
Bài 3: Cho hình vuông ABCD có cạnh a. Trên hai cạnh AB, AD lần lượt lấy hai điểm là M và N sao cho chu vi tam giác AMN là 2a. Tìm vị trí của M và N sao cho SAMN lớn nhất.
Bài 4:Cho tam giác ABC có các cạnh a,b,c. M là điểm nằm trong tam giác. Gọi khoảng cách từ M đến cáccạnh BC,AC,AB lần lượt là x,y,z. Xác định vị trí của điểm M để tổng \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}\) đạt giá trị nhỏ nhất.
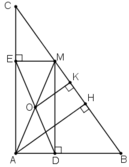
Bài 5: Cho tam giác ABC nhọn. M là điểm nằm trong tam giác. Xác định vị trí của M để MA.BC+MB.AB đạt giá trị nhỏ nhất.
Bài 6: Cho tam giác ABC , M là điểm chuyển động trên cạnh BC, N là điểm trên đoạn thẳng AM sao cho \(\dfrac{AN}{AM}=\dfrac{1}{k}\) (k>1, k cho trước). Qua N kẻ đường thẳng song song với AB cắt AC tại E. Xác định vị trí của điểm M để SADE đạt GTLN.