1. ΔABE = ΔHBE

Xét ΔABE và ΔHBE, ta có :

 (gt)

( BE là đường phân giác BE).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

1. ΔABE = ΔHBE

Xét ΔABE và ΔHBE, ta có :

 (gt)

( BE là đường phân giác BE).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

tick nha

1. ΔABE = ΔHBE

Xét ΔABE và ΔHBE, ta có :

 (gt)

( BE là đường phân giác của góc HBA).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

khó thể xem trên mạng

Hình tự vẽ

a)Xét hai tam giác vuông ABE và HBE CÓ:

AE-chung

góc ABE=góc HBE(gt)

=>tam giác ABE=tam giác HBE(ch-gn)

b)Có tam giác ABE=tam giác HBE(cmt)

=>AB=BH

=>Tam giác BHA cân tại B

mà BE là p/g của góc ABH

=>BE là đường cao, đường trung tuyến

=>BE\(\perp\) AH

c)Xét tam giác AEK và tam giác HEC CÓ

góc KAE=góc EHC=90⁰

AE=EH

góc AEK=góc HEC

=>tam giác AEK= tam giác HEC(c.g.c)

=>EK=EC

d)Xét tam giác EHC có góc EHC=90⁰

=> EC là cạnh lớn nhất

=>EC>EH

Mà EH=AE

=>EC>AE

1. ΔABE = ΔHBE

Xét ΔABE và ΔHBE, ta có :

 (gt)

( BE là đường phân giác BE).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

Xét ΔABE và ΔHBE, ta có :

 (gt)

( BE là đường phân giác BE).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

a) xet tam giac ABE vuong tai A va tam giac HBE vuong tai H ta co

BE=BE ( canh chung) ; goc ABE= goc HBE ( BE la  tia p/g goc B)

--> tam giac ABE= tam giac HBE ( ch=gn)

b) ta co

BA=BH ( tam giac ABE= tam giac HBE)

EA=EH( tam giac ABE= tam giac HBE)

==> BE la duong trung truc cua AH

c) xet tam giac EKA va tam giac ECH   ta co

AE=EH ( tam giacABE= tam giacHBE) ; goc EAK= goc EHC (=90); goc AEK= goc HEC ( 2 goc doi dinh )

--> tam giac EKA = tam giac ECH ( g--c-g)

-->  EK=EC (2 canh tuong ung )

d) tu diem E den duong thang HC ta co :

EH la duong vuong goc ( EH vuong goc BC)

EC la duong xien

-> EH<EC ( quan he duong xien duong vuong goc)

ma EH= AE ( tam giac ABE= tam giac HBE)

nen AE < EC

Cho tam giác ABC vuông tại a ; đường phân giác BE. kẻ EH cuông góc BC(H thuộc BC) Gọi K là giao điểm của AB và HE . Chứng minh rằng  

1) Tam giác ABE=tam giác HBE

2) BE là đường trung trực của đoạn thẳng AH; Chứng minh BE vuông góc KC

3) AE<EC

Đề mình hơi khác các bạn giả hộ mình vs

phần C của mình là so sánh BC vs MH cơ

a) Xét tam giác ABE vuông tại A và ta giác HBE vuông tại H

có: BE là cạnh chung

góc ABE = góc HBE (gt)

\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)

b) ta có: \(\Delta ABE=\Delta HBE\left(pa\right)\)

=> AE = HE ( 2 cạnh tương ứng)

Xét tam giác AEM vuông tại A và tam giác HEC vuông tại H

có: AE = HE ( cmt)

góc AEM = góc HEC ( đối đỉnh)

\(\Rightarrow\Delta AEM=\Delta HEC\left(cgv-gn\right)\)

=> EM = EC ( 2 cạnh tương ứng)

c) Gọi BE cắt CM tại K

ta có: \(\Delta ABE=\Delta HBE\left(pa\right)\)

=> AB = HB ( 2 cạnh tương ứng) (1)

ta có: \(\Delta AEM=\Delta HEC\) ( chứng minh phần b)

=> AM = HC ( 2 cạnh tương ứng) (2)

Từ (1);(2) => AB + AM = HB + HC

                => BM = BC (*)

Xét tam giác BMH vuông tại H

có: BM > MH ( quan hệ cạnh huyền, cạnh góc vuông) (**)

Từ (*), (**) => BC>MH

mk ko bít kẻ hình trên này, sorry bn nha!

a) xét tam giác ABE vuông tại A và tam giác HBE vuông tại H có 

 gócABE = gócHBE ( BE là phân giác gócABH) 

BE chung

 \(=>\)tam giác vuông ABE = tam giác vuông HBE ( cạnh huyền góc nhọn )

\(=>\)AE=EH ( 2 cạnh tương ứng)

b) xét tam giác AKE vuông tại A và tam giác HCE vuông tại H có

AE=EH ( theo câu a)

góc AEK = HEC ( 2 góc đối đỉnh ) 

\(=>\)tam giác vuông AKE = tam giác vuông HCE ( cạnh góc vuông - góc nhọn kề cạnh ấy)

\(=>\)EK=EC ( 2 cạnh tương ứng ) 

a, xét 2 tam giác vuông ABE và HBE có:

          BE cạnh chung

         \(\widehat{ABE}\)=\(\widehat{HBE}\)(gt)

=> tam giác ABE =tam giác HBE(CH-GN)

b) gọi O là giao điểm của BE và AH

xét tam giác OAB và tam giác OHB có:

          OB chung

         \(\widehat{OBA}\)=\(\widehat{OBH}\)(gt)

         AB=HB(theo câu a)

=> tam giác OAB=tam giác OHB(c.g.c)

=> OA=OH=> O là trung điểm của AH(1)

\(\widehat{AOB=\widehat{HOB}}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AOB=\widehat{HOB}}\)=90 độ => BO\(\perp\)AH(2)

từ (1) và (2) => BE là trung trực của AH

c)xét 2 tam giác vuông EAK và HEC có:

       AE=EH

      \(\widehat{AEK=\widehat{HEC}}\)(đối đỉnh)

=> tam giác EAK=tam giác HEC(cạnh góc vuông-góc nhọn)

=> EK=EC

d) trong tam giác vuông AEK có: AE<EK(vì cạnh huyền>cạnh góc vuông) mà EK=EC=> AE<EC

--thanks you very much--

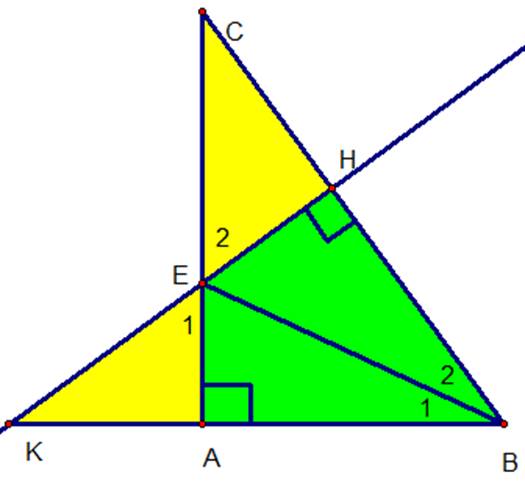
Xét ΔABE và ΔHBE, ta có:

 (gt)

( BE là đường phân giác BE).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

cre baji