Cho tam giác ABC, các đường phân giác góc ngoài tại đỉnh B; C cắt nhau tại K. Đường thẳng vuông góc với AK tại K cắt AB, AC ở D và E. Chứng minh:
a) tam giác DBK đồng dạng với EKC
b) Chứng minh : DE^2 = 4BD . CE

Những câu hỏi liên quan
Cho tam giác ABC và đường phân giác AD, Gọi H,K lần lượt là chân các đường vuông góc kẻ từ B,C xuống đường phân giác ngoài của góc ngoài tại đỉnh A của tam giác ABC. Biết AD=3cm.KH=4cm.Tính Diện tích tam giác ABC?
Cho tam giác ABC có góc C=70 độ , các đường phân giác của góc ngoài tại đỉnh A ,C và đường phân giác trong đỉnh B cắt nhau tại I . Tính góc AIB
+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)
góc A2 = xAC / 2
=> góc A2 = (góc ABC + C1) / 2 = B1 + ( C1 / 2 ) (Vì góc B1 = ABC /2 )
+) Trong tam giác AIB: góc AIB = 180o - (B1 + A1 + A2)
= 180o - (B1 + A1 +B1 + ( C1 / 2 ) )
= 180o - (2.B1 + A1 + ( C1 / 2 ) )
= 180o - (B + A1 + ( C1 / 2 ))
Mà B + A1 = 180o - C1 = 180o - 70o = 110o; C1 / 2 = 70o/ 2 = 35o
=> góc AIB = 180o - (110o + 35o) = 180o - 145o = 35o
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A = 120 độ. Các đường phân giác AD và CE cắt nhau tại O . Đường thẳng chuwas tia phân giác ngoài tại đỉnh B của tam giác ABC cắt đường thẳng tại F. Chứng mình Bo vuông góc với BF và DE là tia phân giác của góc HDB
Các đường phân giác của các góc ngoài ở đỉnh B và C của tam giác ABC cắt nhau tại O.CM: góc BOC bằng nửa góc ngoài ở đỉnh A
1. Cho tam giác ABC, góc A 120 độ, AA, BB, CC theo thứ tự là tia phân giác của các góc A, B, C. CMR AB vuông góc với AC.2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD 1/2 MN.3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
Đọc tiếp
1. Cho tam giác ABC, góc A = 120 độ, AA', BB', CC' theo thứ tự là tia phân giác của các góc A, B, C. CMR A'B' vuông góc với A'C'.
2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD = 1/2 MN.
3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
1.Cho tam giác ABC có góc A bằng 120 độ, đường phân giác AD. Đường phân giác ngoài tại đỉnh C cắt đường thẳng AB tại K. E là giao điểm của DK và AC. Tính góc BED?
2.Cho tam giác ABC có góc A bằng 120 độ, các đường phân giác AD, BE, CF.
a.Chứng minh DE là phân giác ngoài của tam giác ADB
b. Tính góc EDF
Cho tam giác ABC có góc C =70 độ,các đường phân giác của góc ngoài tại đỉnh A,C và phân giác góc trong đỉnh A cắt nhau tại I .Tính góc AIB
+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)
góc A2 = xAC / 2
=> góc A2 = (góc ABC + C1) / 2 = B1 + ( C1 / 2 ) (Vì góc B1 = ABC /2 )
+) Trong tam giác AIB: góc AIB = 180o - (B1 + A1 + A2)
= 180o - (B1 + A1 +B1 + ( C1 / 2 ) )
= 180o - (2.B1 + A1 + ( C1 / 2 ) )
= 180o - (B + A1 + ( C1 / 2 ))
Mà B + A1 = 180o - C1 = 180o - 70o = 110o; C1 / 2 = 70o/ 2 = 35o
=> góc AIB = 180o - (110o + 35o) = 180o - 145o = 35o
Đúng 0
Bình luận (0)
Trần thị Loan là thành viên trong Online Math
Đúng 0
Bình luận (0)
Cho tam giác ABC. Các đường phân, giác các góc ngoài tại đỉnh A và C cắt nhau ở K.a) Cho các tia phân giác các góc A và C trong tam giác ABC cắt nhau ở I Chứng minh B, I, K thẳng hàng.b) Cho biết
A
B
C
^
70
°
. Tính
A
K
C
^
?
Đọc tiếp
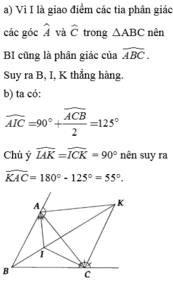
Cho tam giác ABC. Các đường phân, giác các góc ngoài tại đỉnh A và C cắt nhau ở K.
a) Cho các tia phân giác các góc A và C trong tam giác ABC cắt nhau ở I Chứng minh B, I, K thẳng hàng.
b) Cho biết A B C ^ = 70 ° . Tính A K C ^ ?
Cho tam giác ABC, Hai đường phân giác của các cặp góc ngoài đỉnh B và C, đỉnh C và A, đỉnh A và B lần lượt cắt nhau tại A, B, C. Chứng minh rằng AA, BB, CC là các đường cao của tam giác ABC. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác ABC.
Đọc tiếp
Cho tam giác ABC, Hai đường phân giác của các cặp góc ngoài đỉnh B và C, đỉnh C và A, đỉnh A và B lần lượt cắt nhau tại A', B', C'. Chứng minh rằng AA', BB', CC' là các đường cao của tam giác A'B'C'. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'.
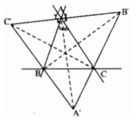
Ta có AA′⊥ AB′ vì chúng là hai tia phân giác của hai góc kề bù. Tương tự AA′⊥ AC′. Vì qua A chỉ có một đường vuông góc với AA' nên ba điểm B', A, C' thẳng hàng và AA′⊥ B′C′, hay A'A là một đường cao của tam giác A'B'C'. Hoàn toàn tương tự ta chứng minh được BB' và CC' là hai đường cao của tam giác A'B'C'.
Mặt khác theo cách chứng minh của bài 9.5 ta có AA', BB', CC' là ba tia phân giác của các góc A, B, C của tam giác ABC. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'.
Đúng 0
Bình luận (0)
cho tam giác ABC, đường phân giác AD. Gọi I, K theo thứ tự là chân các đường vuông góc kẻ từ B và C đến đường phân giác góc ngoài tại đỉnh A. Tính diện tích tam giác ABC biết IK=a ; AD=b