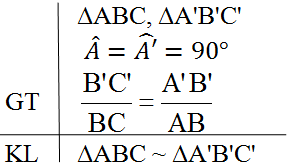Phát biểu định nghĩa hai tam giác đồng dạng ?

Những câu hỏi liên quan
Phát biểu định nghĩa hai tam giác đồng dạng.
Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:
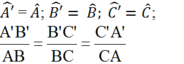
Đúng 0
Bình luận (0)
Phát biểu định lí về ba trường hợp đồng dạng của hai tam giác.
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Đúng 0
Bình luận (0)
Phát biểu các định lí về ba trường hợp đồng dạng của hai tam giác ?
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Đúng 0
Bình luận (0)
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Đúng 0
Bình luận (0)
Phát biểu định lí về trường hợp đồng dạng đặc biệt của hai tam giác vuông (trường hợp cạnh huyền và một cạnh góc vuông).
Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
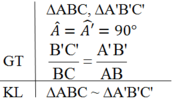
Đúng 0
Bình luận (0)
Phát biểu định lí về trường hợp đồng dạng đặc biệt của hai tam giác vuông (trường hợp cạnh huyền và một cạnh góc vuông) ?
Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Đúng 1
Bình luận (0)
Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Đúng 1
Bình luận (0)
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
Đọc tiếp
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
Nếu hai tam giác đồng dạng với nhau thì: Chọn phát biểu sai trong các phát biểu sau? A. Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng. B. Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng. C. Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng. D. Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng.
Đọc tiếp
Nếu hai tam giác đồng dạng với nhau thì: Chọn phát biểu sai trong các phát biểu sau?
A. Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
B. Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
C. Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
D. Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng.
Áp dụng tính chất mở rộng
Nếu hai tam giác đồng dạng với nhau thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
+ Tỉ số các chu vi bằng tỉ số đồng dạng.
Đáp án D sai.
Chọn đáp án D.
Đúng 0
Bình luận (0)
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh (Vẽ hình)Câu 2: Phát biểu định lí hai góc đối đỉnhCâu 3: phát biểu định nghĩa hai đường thẳng vuông gócCâu 4: Phát biểu định nghĩa đường trung trực của đoạn thẳngCâu 5: Phát biểu dấu hiệu (định lí) nhận bik hai đường thẳng song songCâu 6: Phát biểu tiên đề ơ clít về đường thẳng song songCâu 7: Phát biểu tính chất (định lí) của hai đường thẳng song songCâu 8: Phát biểu định lí về hai đường thẳng phân biệt với một đường thẳng số 3Câu 9: Phát biểu định l...
Đọc tiếp
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh (Vẽ hình)
Câu 2: Phát biểu định lí hai góc đối đỉnh
Câu 3: phát biểu định nghĩa hai đường thẳng vuông góc
Câu 4: Phát biểu định nghĩa đường trung trực của đoạn thẳng
Câu 5: Phát biểu dấu hiệu (định lí) nhận bik hai đường thẳng song song
Câu 6: Phát biểu tiên đề ơ clít về đường thẳng song song
Câu 7: Phát biểu tính chất (định lí) của hai đường thẳng song song
Câu 8: Phát biểu định lí về hai đường thẳng phân biệt với một đường thẳng số 3
Câu 9: Phát biểu định lí về hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba
Câu 10: Phát biểu định lí về một đường thẳng vuông góc với một đường thẳng song song
Câu 11: Phát biểu định lí về tổng ba góc của một tam giác
Câu 12: phát biểu tính chất góc ngoài của tam giác, phát biểu ba trường hợp bằng nhau của tam giác
Câu 13: phát biểu các trường hợp bằng nhau của tam giác vuông
(Mọi người ơi mọi người giúp em mấy câu hỏi này với😅Thank you m.n)
vote cho mk xong rồi mk trả lời cho, tin mk đi, mk ko phải n xấu đâu
Cho tam giác ABC. Từ các mệnh đề
P: “Tam giác ABC có hai góc bằng 60o ”
Q: “ABC là một tam giác đều”
Hãy phát biểu định lí P ⇒ Q. Nêu giả thiết, kết luận và phát biểu lại định lí này dưới dạng điều kiện cần, điều kiện đủ.
P ⇒ Q: “ Nếu tam giác ABC có hai góc bằng 60o thì ABC là một tam giác đều”
Giả thiết: “Tam giác ABC có hai góc bằng 60o ”
Kết luận: “ABC là một tam giác đều”
Phát biểu lại định lí này dưới dạng điều kiện cần: “ABC là một tam giác đều là điều kiện cần để tam giác ABC có hai góc bằng 60o”
Phát biểu lại định lí này dưới dạng điều kiện đủ : “Tam giác ABC có hai góc bằng 60o là điều kiện đủ để ABC là tam giác đều”
Đúng 0
Bình luận (0)