Vẽ hình đối xứng với các hình đã cho qua trục d (h.58)
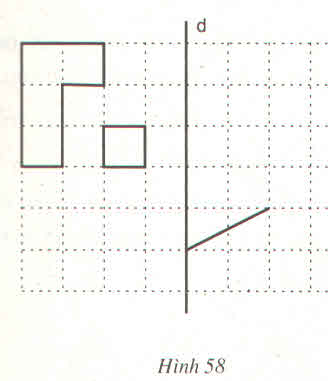
Vẽ hình đối xứng với các hình đã cho qua trục d (h.58).
Cho một đường thẳng trên mặt phẳng. Hãy dựng hình mới là đối xứng của hình vuông đã vẽ qua trục đường thẳng trên. Sử dụng công cụ đối xứng trục để vẽ hình.
Cho một đường thẳng trên mặt phẳng. Hãy dựng hình mới là đối xứng của tam giác đã vẽ qua trục đường thẳng trên. Sử dụng công cụ đối xứng trục để vẽ hình.

Vẽ hình đối xứng qua đường thẳng d của hình đã vẽ (h.6)
- Giả sử AB ∩ d = I; CD ∩ d = H
- Trên tia AB lấy A', B'sao cho IA = IA'; IB = IB'
- Trên tia CD lấy C', D' sao cho HC' = HC; HD' = HD
- Từ E kẻ đường vuông góc với d, cắt d tại J
- Trên EJ lấy E' sao cho JE = JE'
Nối các điểm đã dựng ta được hình đối xứng qua d của hình đã cho.
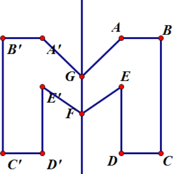
Vẽ hình đối xứng qua đường thẳng d của hình đã vẽ (h.6)
- Kéo dài AB, CD cắt d tại M, Q
- Trên tia AB lấy A', B' sao cho MB' = MB; MA' = MA
- Trên tia CD lấy C', D' sao cho QC' = QC; QD' = QD
- Trên tia EN lấy E' sao cho NE = NE'
- Trên tia FP lấy F' sao cho PF = PF'
Nối các điểm đã dựng ta được hình đối xứng qua d của hình đã cho.
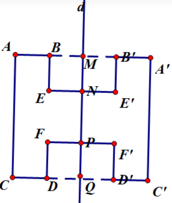
Số phát biểu sai:
a) Phép đối xứng trục là một phép dời hình
b) Đường thẳng d được gọi là trục đối xứng của hình (H) nếu phép đối xứng trục Đd biến hình (H) thành chính nó.
c) Một hình có thể có một hay nhiều trục đối xứng, có thể không có trục đối xứng.
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó.
e) Qua phép đối xứng trục Đa, đường tròn có tâm nằm trên a sẽ biến thành chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó
g) Qua phép đối xứng trục Đa, ảnh của đường thẳng vuông góc với a là chính nó
h) Nều phép đối xứng trục biến đường thẳng a thành đường thẳng b cắt a thì giao điểm của a và b nằm trên trục đối xứng
i) Hình chữ nhật có 4 trục đối xứng
A. 3
B.5
C. 7
D.9
Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng
Cho tam giác ABC nhọn, AB<AC, các đường cao cắt tại H, M là trung điểm của BC. D là điểm đối xứng với H qua M, E là điểm đối xứng với H qua BC. Chứng minh:
a) Tứ giác BHCD là hình bình hành.
b) BAC + BDC= 180
c) Tứ giác BCDe là hình có trục đối xứng.
cho tam giác ABC vuông tại A . Đường cao AH. Gọi D là điềm đối xứng với H qua AB , E đối xứng với H qua AC.
a)Chứng minh :D đối E qua A ( đã biết làm )
b)tam giác DHE là tam giác gì ? vì sao ? ( đã biết làm )
c)tứ giác BDEC là hình gì? vì sao?
d) chứng minh BC=BD+CE
Mình còn mỗi câu c với d . Giải thích cặn cẽ hộ mình với ^^
Hình thì các b tự vẽ hộ được k ạ ? mình k quen cách vẽ ở trên này , vẽ cũng mất có 2p thôi :)
Cho ABC, kẻ AH BC tại H, vẽ điểm D đối xứng với H qua AB, vẽ điểm E đối xứng với H qua AC. Chứng minh ADE cân.
* Có vẽ hình nhé ❤️
chép sai đề bài thì làm sao giải được
sai chỗ này nè
kẻ AH...BC tại H
Cách 1: Vì D đối xứng với H qua AB => AB là đường trung trực DH => AD = AH
E đối xứng với H qua AC => AC là đường trung trực HE => AH = AE
=> AD = AE
=> △AED cân tại A
Cách 2: Gọi AB ∩ DH = { I } , HE ∩ AC = { O }
Vì D đối xứng với H qua AB => AB là đường trung trực DH => AB ⊥ DH tại I và ID = IH
E đối xứng với H qua AC => AC là đường trung trực HE => AC ⊥ HE tại O và HO = OE
Xét △AID và △AIH cùng vuông tại I
Có: ID = IH (cmt)
AI là cạnh chung
=> △AID = △AIH (2cgv)
=> AD = AH (2 cạnh tương ứng)
Xét △AOH và △AOE cùng vuông tại O
Có: OH = OE (cmt)
AO là cạnh chung
=> △AOH = △AOE (2cgv)
=> AH = AE (2 cạnh tương ứng)
Mà AH = AD (cmt)
=> AE = AD
=> △AED cân tại A