Chứng minh rằng diện tích tam giác nội tiếp trong hình bình hành (tam giác có 3 đỉnh nằm trên các cạnh của hình bình hành) không lớn hơn nửa diện tích của hình bình hành.
Giải hộ mik nha!!!
Những câu hỏi liên quan
Chứng minh rằng diện tích một hình bình hình nằm trong một tam giác không lớn hơn nửa diện tích tam giác đó
Hình bình hành ABCD có 4 đỉnh lần lượt nằm trên các cạnh tứ giác EFGH, trong đó có 2 điểm là trung điểm của 2 cạnh tứ giác. Chứng minh diện tích hình bình hành ABCD = \(\frac{1}{2}\)diện tích tứ giác EFGH
Cho hình bình hành ABCD, các điểm E và F nằm trên
cạnh AB. Tam giác GDC là tam giác vuông tại C. Biết
DC = 8cm, GC = 7 cm. Tổng diện tích hai tam giác
AED và BFC lớn hơn diện tích tam giác GEF là 12
cm2
. Tính diện tích hình bình hành ABCD
giúp mình đi mình tick đúng chooo!! cíuuuu
Chứng minh rằng :diện tích tam giác có ba đỉnh nằm trên ba cạnh của hình vuông bao giờ cũng bé hơn một nửa diện tích hình vuông đó {đỉnh tam giác không trùng với đỉnh hình vuông
ko biet dau , mk dang hoc lop 5 len 6 nen ko biet lam
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
5) Trên cạnh AB và CD của hình bình hành ABCD lần lượt lấy hai điểm M và N sao cho AM = CN, P là điểm trên AD, các đường thẳng MN, BP, CP chia hình bình hành thành ba tam giác và ba tứ giác. Chứng minh rằng trong đó diện tích một tam giác bằng tổng diện tích hai tam giác còn lại, và diện tích một tứ giác bằng tổng diện tích hai tứ giác còn lại.
1.Chứng minh nếu 1 hình bình hành và tam giác có cùng cạnh đáy và chiều cao thì diện tích hình bình hành bằng 2 lần diện tích tam giác
2. Cho hình bình hành ABCD, O nằm trong hình bình hành. chứng minh SAOB +SCOD=SAOD + SBOC
chiều dài độ đáy hình bình hành là 16 cm
Đúng 0
Bình luận (0)
chứng minh rằng diện tích tam giác có ba đỉnh nằm trên ba cạnh một hình vuong bao giờ cũng bé hơn một nửa diện tích hình vuông (đỉnh tam giác không trùng với định hình vuông
Cho hình bình hành ABCD vẽ đường thẳng xy qua A không cắt đường chéo BD. Gọi E là 1 điểm trên xy, E nằm ngoài hình bình hành ABCD. Chứng minh diện tích tam giác AEC = diện tích tam giác ABE + diệm tích tam giác ADE.
Giúp mình nhanh nhé !Cảm ơn các bạn nhiều !
Gọi O là giao điểm của AC và BD. Theo tính chất hình bình hành thì O là trung điểm AC và BD.
Gọi H, I, J, L lần lượt là chân các đường cao hạ từ D, O, C, B xuống đường thẳng xy.
Ta thấy ngay DH // OI // CJ // KB.
Xét tam giác ACJ có O là trung điểm AC, OI // CJ nên OI là đường trung bình tam giác hay CJ = 2OI. (1)
Xét hình thang vuông HDBK có O là trung điểm BD, OI // DH // BK nên OI là đường trung bình hình thang.
Vậy thì \(DH+BK=2OI\) (2)
Từ (1) và (2) suy ra CJ = DH + BK.
Suy ra \(\frac{1}{2}CJ.AE=\frac{1}{2}HD.AE+\frac{1}{2}BK.AE\) hay \(S_{ACE}=S_{ADE}+S_{ABE}\)
Đúng 0
Bình luận (0)
1
Ta có do \(K\in CD;CD//AB\Rightarrow\widehat{K1}=\widehat{A2}\)
Mà \(\widehat{A2}=\widehat{A1}\)(AK LÀ PHÂN GIÁC)
\(\Rightarrow\widehat{K1}=\widehat{A1}\Rightarrow\Delta ADK\)cân tại D => AD=DK
Tương tự ta cm được BC=CK
=> AD+BC=DK+CK
Mà K nằm giữa C và D nên AD+BC=DK+CK=DC(đpcm)
Đúng 0
Bình luận (0)
Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO.
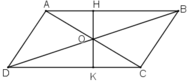
Gọi OH, OK lần lượt là chiều cao của tam giác AOB và tam giác DOC.
Ta có: OK ⊥ CD, CD // AB ⇒ OK ⊥ AB ⇒ O, H, K thẳng hàng.
Do đó:
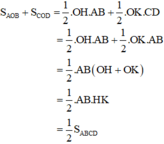
Mà SABCD = SAOB + SBOC + SCOD + SDOA
Do đó SAOB + SCOD = SBOC + SDOA.
Đúng 0
Bình luận (0)