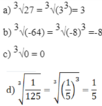Căn bậc hai số của 64 có thể viết \(\sqrt{64}=6+\sqrt{4}\). Tìm tất cả các số tự nhiên có 2 chứ số viết được căn bậc hai của chúng duới dạng trên và là một số nguyên
Gọi số đó là 10a+b (a, b nguyên; 0<a<10; 0<=b<10)
Khi đó: √(10a+b) = a + √b
Để √(10a+b) nguyên thì √b nguyên <=> b = 1 hoặc 4 hoặc 9
Bình phương hai vế => a^2 - (10-2√b)a = 0
<=> a(a-10+2√b) = 0
a = 0 (loại)
=> a-10+2√b = 0 <=> a = 10-2√b
+) b = 1 <=> a = 8 => 81 thỏa mãn
+) b = 4 <=> a = 6 => 64 thỏa mãn
+) b = 9 <=> a = 4 => 49 thỏa mãn
ok bạn nhá
Tính giá trị biểu thức :
a) căn bậc hai 1,6 trên 2,5 - 0,4 . 4,25
b) 3/4 - căn bậc hai 3/12 + căn bậc hai 9/4
c) 4 và 1/3 - căn bậc hai 16 + 5 căn bậc hai 4/9 - 25/ căn bậc hai 36
d) căn bậc hai 0,36 trên 0,47 : căn bậc hai 64/14- căn bậc hai 49/9 + 3 / căn bậc hai 25 : 3/100
MÌNH ĐANG CẦN GẤP , LÀM XONG ĐẦU TIÊN VÀ CHÍNH XÁC MÌNH TRẢ 5 TICK!!!
Căn bậc hai của 64 có thể viết dưới dạng như sau √64=6+√4.Hỏi có tồn tại hay ko các số có 2 chữ số có thể viết căn bậc hai của chúng dưới dạng như trên và là một số nguyên? hãy chỉ ra toàn bộ các số đó
căn bậc 2 của 64 có thể viết dưới dạng như sau: \(\sqrt{64}=6+\sqrt{4}\) hỏi có tồn tại hay không các chữ số có thể viết căn bậc 2 của chúng dưới dạng như trên và là 1 số nguyên?
Gọi số đó là 10a+b (a, b nguyên; 0<a<10; 0<=b<10)
Khi đó: √(10a+b) = a + √b
Để √(10a+b) nguyên thì √b nguyên <=> b = 1 hoặc 4 hoặc 9
Bình phương hai vế => a^2 - (10-2√b)a = 0
<=> a(a-10+2√b) = 0
@1: a = 0 (loại)
@2: a-10+2√b = 0 <=> a = 10-2√b
+) b = 1 <=> a = 8 => 81 thỏa mãn
+) b = 4 <=> a = 6 => 64 thỏa mãn
+) b = 9 <=> a = 4 => 49 thỏa mãn
Kết luận: ...
Đúng 2
Bình luận (0)
Tìm căn bậc ba của mỗi số sau: -64
căn bậc 3 của 64 bằng
căn bậc hai của 64 có thể viết dưới dạng như sau:\(\sqrt{64}+6+\sqrt{4}\)
hỏi có tồn tại hay không các số có 2 chữ số có thể viết căn bậc hai của chúng dưới dạng nhhư trên và là 1 số nguyên ? hãy chỉ ra 2 số đó
Căn bậc hai của 64 có thể viết dưới dạng như sau: \(\sqrt{64}=6+\sqrt{4}\)
Hỏi có tồn tại hay không các số có hai chữ số có thể viết căn bậc hai của chúng dười dạng như trên và là một số nguyên, hãy chỉ ra toàn bộ các số đó.
Help me!!!
Căn bậc hai của 64 có thể viết dưới dạng như sau: sáu + căn 4
Hỏi coa tồn tại hay không các số có hai chữ số có thể viết căn bậc hai của chúng dưới dạng như trên và là một số nguyên? Hãy chỉ ra toàn bộ các số đó?
Tìm căn bậc ba của mỗi số sau
a) 27; b) -64; c) 0; d) 1/125