Cho hình thang ABCD (AB//CD ) 2 đường chéo cắt nhau tại O . Trên đáy CD lấy các điểm E và F sao cho OE//AD ; Ò // BC . CMR :
Diện tích ODE = S OCF
3: Cho hình thang ABCD (AB // CD) hai đường chéo cắt nhau tại O. Trên đáy CD
lấy các điểm E và F sao cho OE // AD; OF // BC. Chứng minh rằng \(S_{ODE}=S_{OCF}\)
1.Cho hình thang ABCD (AB//CD) có 2 đường chéo cắt nhau tại O .Trên đáy lớn CD lấy 2 điểm E và F sao cho OE//AD,OF//BC.Chứng minh DE=CF
2.Cho hình thang ABCD (BC// AD và BC <AD).Gọi M,N là các điểm trên 2 cạnh AB,BC sao cho AM/AB=CN/CD.Đường thẳng MN cắt AC và BD thứ tự tại E và F.Chứng minh ME=NF
3.Cho góc xOy.Gọi M,N là 2 điểm theo thứ tự di động trên Ox và Oy sao cho a/OM+b/ON=1,trong đó a,b là các số dương cho trước.Chứng minh đường thẳng MN luôn đu qua 1 điểm cố định
Bạn tự vẽ hình nhé
Xét \(\Delta ACD\) có OE // CD(gt)
=> \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét \(\Delta BCD\) có OF // CD (gt)
=> \(\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)\)
Mặt khác AB // CD nên \(\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
=> \(\dfrac{OE}{DC}=\dfrac{OF}{DC}\) => OE = OF
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF
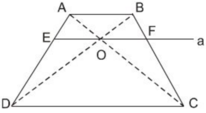
cho hình thang abcd. gọi m là trung điểm của ab, n là trung điểm của cd. lấy o bất kỳ trên mn, kẻ đường thẳng qua o // với 2 đáy ab và cd cắt ad tai e và cắt bc tại f. Chứng minh oe=of
Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và F
Chứng minh rằng OE = OF.
Tam giác ABD có OE//AB
=>DO/DB = OE/AB (Theo hệ quả Đlý Ta-lét) (1)
Tam giác ABC có OF//AB
=>CO/CA = OF/AB (Theo hệ quả Đlý Ta-lét) (2)
Tam giác ABO có CD//AB
=>OD/OB = OC/OA (Theo hệ quả Đlý Ta-lét)
=> OD/(OB+OD) = OC/(OA+OC) hay OD/DB=CO/CA (3)
Từ (1) (2) và (3)
=> OE/AB = OF/AB
=> OE = OF (đpcm.)
Bài 1: Cho hình thang cân ABCD (AB//CD;AB⊥CD).Vẽ E đối xứng A qua CD, F đối xứng A qua trung điểm M của CD. Chứng minh A,B,C,D,E,F cùng thuộc một đường tròn.
Bài 2 : Cho hình thoi ABCD , 2 đường chéo cắt nhau tại O. Trên AB,BC lấy các điểm E,F sao cho BE=BF. OE cắt CD tại G, OF cắt AB tại H. Chứng minh E,F,G,H cùng thuộc 1 đường tròn
Mọi người giúp em với ạ, mai e phải nộp rồi :(
Cho hình thang ABCD ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Chứng minh OE = OF.
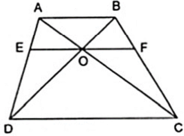
Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
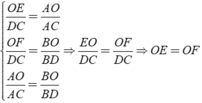
Điều phải chứng minh.