cho tam giac ABC trên mỗi cạnh của hình tam giác ta lấy một điểm rồi nói 3 điểm đó với nhau trên mỗi cạnh của tam giác vừa tạo thành ta lại lấy 1 điểm rồi nói ba điểm đó ới nhau tiếp tục như hệ đến lần thứ ba thì dừng lại ói ở áo nhiều hình tam giác được tạo ra

Những câu hỏi liên quan
Cho hình tam giác ABC trên mỗi cạnh của tam giác ta lấy 1 điểm rồi nói 3 điểm đó với nhau .Trên mỗi cạnh của tam giác vừa tạo thành ta lấy 1 điểm rồi nói 3 điểm đó với nhau.Tiếp tục như thế đến lần thứ 3 thì dừng lại.Hỏi có bao nhiêu tam giác được tạo thành trên hình vẽ?
Cho tam giác ABC. Trên mỗi cạnh của hình tam giác ta lấy một điểm rồi nối 3 điểm đó với nhau. Trên mỗi cạnh của hình tam giác vừa tạo thành ta lại lấy một điểm rồi nối 3 điểm đó với nhau. Tiếp tục như thế đến lần thứ ba thì dừng lại. Hỏi có tất cả bao nhiêu hình tam giác được tạo thành ?
Khi nối lần thứ nhất ta được thêm 4 hình tam giác mới.
Khi nối lần thứ hai mỗi hình tam giác lại tạo thành 4 hình tam giác mới nữa, ...
Sau 3 lần nối như thế thì số tam giác tạo thành là :
1 + 4 + 4 x 4 + 4 x 4 x 4 = 85 (hình tam giác).
Đúng 2
Bình luận (0)
Cho tam giác ABC. Trên mỗi cạnh của tam giác ta lấy một điểm rồi nối 3 điểm đó với nhau. Trên các cạnh của mỗi tam giác vừa tạo thành ta lại lấy một điểm rồi nối 3 điểm đó với nhau. Tiếp tục như thế 3 lần thì dừng lại. Hỏi khi đó ta đếm được tất cả bao nhiêu tam giác ?
đầu tiên ta có một hình tam giác , sau mỗi lần vẽ ta có thêm 4 hình tam giác ( không tin tự vẽ hình ra xem )
Vậy vẽ tiếp tục như thế 3 lần thì dừng lại ta được số tam giác là : 1+4+4+4+4+4= 25 tam gíac
Cho 1 lục giác đều nội tiếp đường tròn . trên mỗi cạnh của lục giác ; ta dựng 1 hình tam giác sao cho 2 cạnh của tam giác không thuộc về phía đường tròn . Lấy tâm đường tròn ngoại tiếp của mỗi tam giác . Chứng minh : 6 điểm đó đồng quy với nhau và tạo thành 1 đường tròn
đây ko phải toán lớp 1 nha
tui lớp 4 ko giải đc mà bảo toán lớp 1😮
đây là toán lớp ....
Xem thêm câu trả lời
Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
A
.
2
45
B
.
9
34
C
....
Đọc tiếp
Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
A . 2 45
B . 9 34
C . 2 5
D . 4 15
Chọn D
Cách 1:
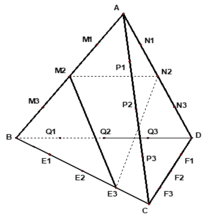
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. C 6 3 = 6 cách.
Suy ra số tam giác thỏa mãn là C 18 3 - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có C 6 1 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
![]()
- Giả sử ta chọn cạnh M 2 N 2 là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do M 2 N 2 ⊂ (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm E 2 , F 2 , P 2 . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là M 2 N 2 và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
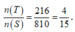
Cách 2: Lưu Thêm
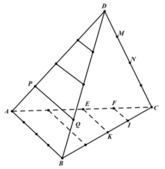
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Trong số C 18 3 đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = C 18 3 - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có ![]()
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy 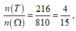
Đúng 0
Bình luận (0)
Gọi ABC là tam giác thứ nhất. Nói điểm chính giữa các cạnh của tam giác AbC ta được tam giác thứ hai.Nói điểm chính các cạnh của tam giác thứ hai ta được tam giác thứ ba. Và cứ tiếp tục về như vậy mãi. Hoi :a) Theo đề trên hay tự vẽ hìnhb) Co tất cả bao nhiêu tam giác trên hình vẽ khi ta về như vậy đến tam giác thứ 20?C) Cho biết diện tích tam giác AbCbang 64 Tính S hình thang trên hình đó(các bn có thể đặt là aBPN)
Đọc tiếp
Gọi ABC là tam giác thứ nhất. Nói điểm chính giữa các cạnh của tam giác AbC ta được tam giác thứ hai.Nói điểm chính các cạnh của tam giác thứ hai ta được tam giác thứ ba. Và cứ tiếp tục về như vậy mãi. Hoi :
a) Theo đề trên hay tự vẽ hình
b) Co tất cả bao nhiêu tam giác trên hình vẽ khi ta về như vậy đến tam giác thứ 20?
C) Cho biết diện tích tam giác AbCbang 64 Tính S hình thang trên hình đó(các bn có thể đặt là aBPN)
ngọc anh , tớ cũng muốn giúp cậu lắm nhưng tớ ko bít làm đành chịu thôi
Đúng 0
Bình luận (0)
một hình tam giác ABC ,trên cạnh BC lấy 10 điểm không trùng nhau . Nối điểm A với các diểm đó .Hỏi có bao nhiêu hình tam giác tạo thành
Cho tam giác ABC. Trên cạnh BC lấy điểm M sao cho CM gấp 3 lần BM. Trên một cạnh khác của tam giác lấy điểm N là trung điểm của cạnh đó.
a) Hãy vẽ hình và nối hai điểm M với N?
b) Tính diện tích của hình tứ giác tạo thành trong các trường hợp trên, biết diện tích hình tam giác ABC là 80 m2
Phần a bạn tự làm nha!
b, Gỉa sử điểm N nằm trên cạnh AC thì ta có:
Smnc / Sabc = cn / ca * cm / cb = 1/2 * 3/4 = 3/8
Suy ra Smnc là: 80 : 8 * 3 = 30 [ m vuông ]
Vậy diện tích hình tứ giác là:
80 - 30 = 50 [ m vuông ]
Đ/S: 50 m vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC. Trên cạnh BC ta lấy 6 điểm. Nối đỉnh A với mỗi điểm vừa chọn. Hỏi đếm được bao nhiêu hình tam giác.


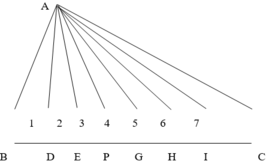
Ta nhận xét :
- khi lấy 1 điểm thì tạo thành 2 tam giác đơn ABD và ADC. Số tam giác đếm được là 3 : ABC, ADB và ADC. Ta có : 1 + 2 = 3 (tam giác)
- khi lấy 2 điểm thì tạo thành 3 tam giác đơn và số tam giác đếm được là 6 :
ABC, ABD, ADE, ABE, ADC và AEC. Ta có : 1+ 2 + 3 = 6 (tam giác)
Vậy khi lấy 6 điểm ta sẽ có 7 tam giác đơn được tạo thành và số tam giác đếm được là : 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (tam giác)
Cách 2 :- Nối A với mỗi điểm D, E, …, C ta được một tam giác có cạnh AD. Có 6 điểm như vậy nên có 6 tam giác chung cạnh AD (không kể tam giác ADB vì đã tính rồi)
Lập luận tương tự như trên theo thứ tự ta có 5, 4, 3, 2, 1 tam giác chung cạnh AE, AP, …, AI.
Vậy số tam giác tạo thành là : 7 + 6 + 5 + 4 +3 +2 + 1 = 28 (tam giác).
Đúng 1
Bình luận (0)



















