từ tỉ lệ thức a/b=c/d hãy rút ra tỉ lệ thức ;a+c/a-c=b+d/b-d
Từ tỉ lệ thức a/b=c/d hãy rút ra tỉ lệ thức a+c/a-c=b+d/b-d
Theo tính chất của dãy tỉ số bằng nhau, ta có: a/b = c/d = ( a + c )/( b + d ) = ( a - c )/( b - d ) => ( a + c )/( a - c ) = ( b + d )/( b - d )
Từ tỉ lệ thức a b = c d a ≠ c , b ≠ ± d hãy rút ra tỉ lệ thức:
a + c a - c = b + d b - d
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
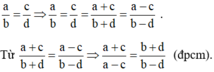
từ tỉ lệ thức a/b = c/d (a # c , b# +- d ) hãy rút ra tỉ lệ thức a+c /a-c = b+d / b-d
a/b=c/d =>a+c/b+d=a-c/b-d=>a+c/a-c=b+d/b-d
từ tỉ lệ thức a/b=c/d(a khác c,b khác d ) hãy rút ra tỉ lệ thức a+c/a-c=b+d/b-d
từ tỉ lệ thức a/b-c/d hãy suy ra tỉ lệ thức a/c=b/d
Từ tỉ lệ thức a/b=c/d
Hãy suy ra tỉ lệ thức 2009a-b/a=2009c-d/c
Cho a,b,c,d khác 0.Từ tỉ lệ thức a/b=c/d hãy suy ra tỉ lệ thức a-b/a=c-d/c
\(\frac{a}{b}=\frac{c}{d}\)
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất dya4 tỉ số bằng nhau:
\(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
\(\Rightarrow\frac{a}{c}=\frac{a-b}{c-d}\Rightarrow\frac{a-b}{a}=\frac{c-d}{c}\left(đpcm\right)\)
ab =cd
⇒ac =bd
Áp dụng tính chất dãy tỉ số bằng nhau:
ac =bd =a−bc−d
⇒ac =a−bc−d ⇒a−ba =c−dc (đpcm)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=cb\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\Rightarrow\frac{a}{c}=\frac{a-b}{c-d}\Rightarrow\frac{a-b}{a}=\frac{c-d}{c}\)
=> đpcm
cho a,b,c,d khác 0 , từ tỉ lệ thức a/b = c/d , hãy suy ra tỉ lệ thức a-b / a = c-d / c
d) a/b = c/d => ad = bc => b/a = d/c
=>b/a - 1 = d/c - 1
b/a - a/a = d/c - c/c
(b - a)/b = (d - c)/c
Cho a,b,c,d khác 0. Từ tỉ lệ thức a/b=c/d hãy suy ra tỉ lệ thức a-b/a=c-d/c
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
=>\(\frac{a}{c}=\frac{a-b}{c-d}\Rightarrow\frac{a-b}{a}=\frac{c-d}{c}\)
Vậy ta có đpcm
có \(\frac{a}{b}=\frac{c}{d}=>\frac{a}{c}=\frac{b}{d}\)
áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
=> \(\frac{a}{c}=\frac{a-b}{c-d}=>\frac{c-d}{c}=\frac{a-b}{a}\)
a/b =c/d ⇒a/c =b/d
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a/c =b/d =a−b/c−d
=>a/c =a−b/c−d ⇒a−b/a =c−d/c
Vậy ta có đpcm