Cần gấp!!!
Cho tam giác ABC vuông tại C.Vẽ về phía ngoài của tam giác ABC các hình vuông ABDE;BCHK;ACFG
Chứng minh:SABDE=SBCHK+SACFG
(Ghi chú:Đây là bài toán chứng minh định lý Py-ta-go nên không sử dụng định lý Py-ta-go để giải bài toán)
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác vẽ các hình vuông ABDE, ACFG và BCHI A.
S
A
C
F
G
S
B
C
H
I
+
S
A
B
D...
Đọc tiếp
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác vẽ các hình vuông ABDE, ACFG và BCHI
A. S A C F G = S B C H I + S A B D E
B. S B C H I = S A B D E + S A C F G
C. S A B D E = S B C H I + S A C F G
D. S B C H I = S A C F G - S A B D E
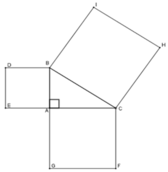
Ta có: SBCHI = BC2; SACFG = AC2; SABDE = AB2
Theo định lý Pytago cho tam giác ABC vuông tại A ta có: BC2 = AB2 + AC2
=> SBCHI = SACFG + SABDE
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A vẽ phía ngoài tam giác ABC các hình vuông ABDE ACFG BCMN đường cao AH của tam giác ABC giao MN tại K CM diện tích của ABDE = diện tích của BHKN
Cho tam giác vuông tại ABC. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Biết
S
B
C
H
I
100
c
m
2
, tính
S
A
C
F
G
+
S...
Đọc tiếp
Cho tam giác vuông tại ABC. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Biết S B C H I = 100 c m 2 , tính S A C F G + S A B D E
A. S A C F G + S A B D E = 200 c m 2
B. S A C F G + S A B D E = 150 c m 2
C. S A C F G + S A B D E = 100 c m 2
D. S A C F G + S A B D E = 180 c m 2
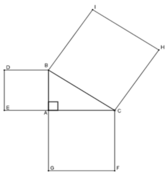
Ta có: SBCHI = BC2; SACFG = AC2; SABDE = AB2
Theo định lý Pytago cho tam giác ABC vuông tại A ta có: BC2 = AB2 + AC2
=> SBCHI = SACFG + SABDE
Vậy SACFG + SABDE = SBCHI = 100 cm2
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho tam giác ABC ( góc A=90 độ ).Vẽ về phía ngoài tam giác ABC các hình vuông ABDE,ACFG. Gọi M là trung điểm của DF.Ch/m tam giác MBC vuông cân
Cho tam giác ABC. Về phía ngoài tam giác dựng các hình vuông ABDE, ACFG. Chứng minh rằng đường cao AH của tam giác ABC đi qua trung điểm M của đoạn thẳng EG.
Cho tam giác ABC (A<90độ). Về phía ngoài của tam giác ABC dựng các hình vuông ABDE, ACFG.?
Gọi M là trung điểm của đoạn thẳng DF. Chứng minh rằng tam giác MBC vuông cân đỉnh M
Cho tam giác ABC. Trên AB,AC về phía ngoài của tam giác dựng các hình vuông ABDE, ACMN. C/m: Trung tuyến qua A của tam giác AEN kéo dài chính là đường cao của tam giác ABC.
cho tam giác ABC nhọn. về phía ngoài tam giác ABC vẽ hình vuông ABDE và hình vuông ACFG. vẽ AH vuông góc với BC, EI vuông góc với AH tại I, GJ vuông góc với AH tại J.
a) CM tam giác ABH tam giác EAI
b)CM AK là trung tuyến tam giác AEG(AH cắt EG tại K)
c)L là điểm thuộc AK sao cho K là trung điểm của AL. CM AL BC
d) CM tam giác ABLtam giác BDC
e)CM CD là đường cao của tam giác BCL
mọi người giúp mình câu e với!!!
Đọc tiếp
cho tam giác ABC nhọn. về phía ngoài tam giác ABC vẽ hình vuông ABDE và hình vuông ACFG. vẽ AH vuông góc với BC, EI vuông góc với AH tại I, GJ vuông góc với AH tại J.
a) CM tam giác ABH = tam giác EAI
b)CM AK là trung tuyến tam giác AEG(AH cắt EG tại K)
c)L là điểm thuộc AK sao cho K là trung điểm của AL. CM AL = BC
d) CM tam giác ABL=tam giác BDC
e)CM CD là đường cao của tam giác BCL
mọi người giúp mình câu e với!!!
CHo tam giác ABC ( góc A nhỏ hơn 90 độ). Về phía ngoài của tam giác ABC dựng các hình vuông ABDE, ACFG. Gọi M là trug điểm của đoạn thẳng DF
a) trên đường thẳng vuông góc vs BC tại B, lấy điểm H sao cho HB=BC. CMR tam giác BHD= tam giác BCA
cho tam giác abc. Vẽ về phía ngoài của tam giác các hình vuông abde , acfg.
a) chứng minh đường cao ah của tam giác abc đi qua trung điểm m của đoạn eg
b) cmr nếu góc a<90 độ và n là trung điểm của df thì tam giác nbc vuông cân tại đỉnh n