Cho tam giác ABC có BN và CM là 2 đường phân giác vuông góc với nhau. Biết AB=19; AC=22. Tính độ dài BC

Những câu hỏi liên quan
Cho tam giác ABC có 2 đường phân giác BN và CM vuông góc với nhau. Biết AB=19; AC=22. Tính độ dài BC
cho tam giác ABC có AB=19; AC=22 kẻ hai đường trung tuyến BN và CM vuông góc với nhau. Tính BC
Gọi giao điểm của BN, CM là G => G là trọng tâm của tam giác ABC
Ta có: BN vuông góc vs CM
=> BG vuông góc vs GM và CG vuông góc vs GN
=> MG2 + GB2 = BM2 =(1/2.AB)2 =90,25 và CG2 + GN2 = NC2 = (1/2AC)2 = 121 (ĐL Pytago)
=> MG2 + GB2 + CG2 + GN2 = 211,25
Mà MG = 1/2 CG và NG = 1/2 BG (Vì G là trọng tâm)
=> (1/2CG)2 + CG2 + (1/2 BG)2 + BG2 =211,25 => 5/4 BG2 + 5/4 CG2 =211,25
=> BG2 +CG2 = 211,25 : 5/4 =169
=> BC2 = 169 (Vì BG2 +CG2 = BC2) => BC = 13
Đúng 0
Bình luận (0)
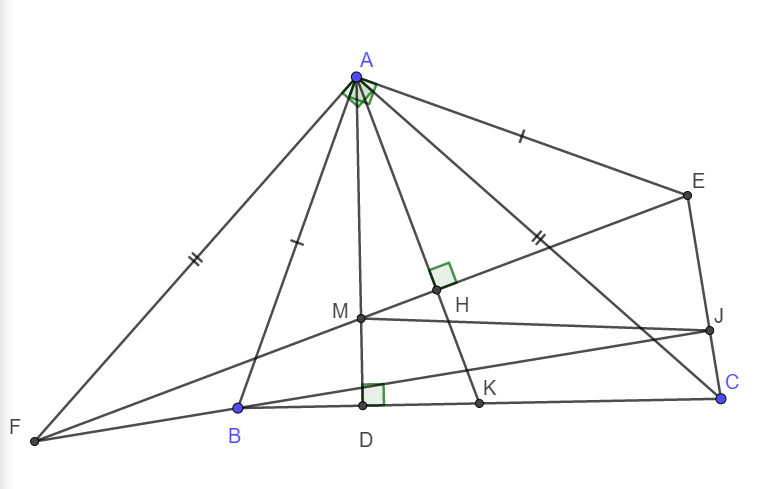
Cho tam giác ABC nhọn có 2 đường cao BD và CE. Tia phân giác của các góc ABD và ACE cắt nhau tại O và lần lượt cắt AC, AB tại N,M. Tia BN cắt CE tại K, tai CM cắt BD tại H. Chứng minh:
a) BN vuông góc với CM.
b) Tứ giác MNHK là hình thoi
cíu iêm với ;-;
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.Bài 2: Cho tam giác ABC có góc A 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM...
Đọc tiếp
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.
Bài 2: Cho tam giác ABC có góc A= 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.
Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM vuông góc với CN.
Mọi người giúp mình nhanh nha😙😙😙😙
Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC có 3 đường trung tuyến AD , BE , CF cắt nhau tại G . Chứng minh rằng a, frac {AB+AC}{2}b,BE+CF frac{3}{2}BCc, frac{3}{4}(AB+BC+AC)AD+BE+CFAB+BC+ACBài 2 : Cho tam giác ABC , tia phân giác góc B , C cắt nhau tại O . Từ A vẽ một đường thẳng vuông góc với OA , cắt OB , OC tại M,N . Chứng minh : BM vuông góc với BN . CM vuông góc với CNBài 3 . Cho tam giác ABC , góc B 450 , đường cao AH , phân giác BD của tam giác ABC , biết góc BDA 450 . Chứng minh HD//AB Bài 4 . Cho tam...
Đọc tiếp
Bài 1 : Cho tam giác ABC có 3 đường trung tuyến AD , BE , CF cắt nhau tại G . Chứng minh rằng
\(a, \frac {AB+AC}{2}\)
\(b,BE+CF < \frac{3}{2}BC\)
\(c, \frac{3}{4}(AB+BC+AC)<AD+BE+CF<AB+BC+AC\)
Bài 2 : Cho tam giác ABC , tia phân giác góc B , C cắt nhau tại O . Từ A vẽ một đường thẳng vuông góc với OA , cắt OB , OC tại M,N . Chứng minh : BM vuông góc với BN . CM vuông góc với CN
Bài 3 . Cho tam giác ABC , góc B = 450 , đường cao AH , phân giác BD của tam giác ABC , biết góc BDA = 450 . Chứng minh HD//AB
Bài 4 . Cho tam giác ABC không vuông , các đường trung trực của AB , AC cắt nhau tại O , cắt BC theo thứ tự M,N . Chứng minh AO là phân giác của góc MAN .
Bài 5 : Cho tam giác ABC nhọn , đường cao BD , CE cắt nhau tại H . Lấy K sao cho AB là trung trực của HK . Chứng minh góc KAB = góc KCB
Cho tam giác ABC, các đường trung tuyến BN và CM vuông góc với nhau.Nếu AB=19, AC=22 thì độ dài cạnh BC là...
Cho tam giác ABC vuông tại A có ABAC , kẻ đường phân giác BD của góc ABC ( D thuộc AC ) . Kẻ DM vuông góc với BC tại M â) Cm: tam giác DAB tam giác DMBb) CM: BD là đường trung trực của AM c) Gọi K là giao điểm của đường thẳng DM và AB , đường thẳng BD cắt KC tại N . CM: BN vuông góc Kc và tam giác KBC cân tại B đ) gọi E al trunbg điểm của BC . Qua N kẻ đường thẳng song song với BC , cắt AB tại P . CM : 3 duog thằng CP , KỆ , BN đồng quy
Đọc tiếp
Cho tam giác ABC vuông tại A có AB<AC , kẻ đường phân giác BD của góc ABC ( D thuộc AC ) . Kẻ DM vuông góc với BC tại M
â) Cm: tam giác DAB = tam giác DMB
b) CM: BD là đường trung trực của AM
c) Gọi K là giao điểm của đường thẳng DM và AB , đường thẳng BD cắt KC tại N . CM: BN vuông góc Kc và tam giác KBC cân tại B
đ) gọi E al trunbg điểm của BC . Qua N kẻ đường thẳng song song với BC , cắt AB tại P . CM : 3 duog thằng CP , KỆ , BN đồng quy
a.Xét ΔDAB,ΔDMBΔ���,Δ��� có:
ˆDAB=ˆDMB(=90o)���^=���^(=90�)
Chung BD��
ˆABD=ˆMBD���^=���^
→ΔDAB=ΔDMB→Δ���=Δ���(cạnh huyền-góc nhọn)
b.Từ câu a →BA=BM,DA=DM→��=��,��=��
→B,D∈→�,�∈ trung trực AM��
→DB→�� là trung trực AM��
c.Ta có: DM⊥BC→KD⊥BC��⊥��→��⊥��
CA⊥AB→CD⊥BK��⊥��→��⊥��
→D→� là trực tâm ΔBCKΔ���
→BD⊥CK→��⊥��
→BN⊥KC→��⊥��
Xét ΔBMK,ΔBACΔ���,Δ��� có:
Chung ^B�^
BM=BA��=��
ˆBMK=ˆBAC(=90o)���^=���^(=90�)
→ΔBMK=ΔBAC(c.g.c)→Δ���=Δ���(�.�.�)
→BK=BC→��=��
→ΔKBC→Δ��� cân tại B�
d.Ta có: ΔBCKΔ��� cân tại B,BN⊥CK→N�,��⊥��→� là trung điểm KC��
Trên tia đối của tia NP�� lấy điểm F� sao cho NP=NF��=��
Xét ΔNKP,ΔNCFΔ���,Δ��� có:
NK=NC��=��
ˆKNP=ˆCNF���^=���^
NP=NF��=��
→ΔNKP=ΔNCF(c.g.c)→Δ���=Δ���(�.�.�)
→KP=CF,ˆNKP=ˆNCF→KP//CF→CF//BP→��=��,���^=���^→��//��→��//��
Xét ΔFPC,ΔBPCΔ���,Δ��� có:
ˆCPF=ˆPCB���^=���^ vì NP//BC��//��
Chung NP��
ˆPCF=ˆCPB���^=���^ vì BP//CF��//��
→ΔFPC=ΔBCP(g.c.g)→Δ���=Δ���(�.�.�)
→CF=BP→��=��
→PK=BP→��=��
→P→� là trung điểm BK��
Do E,N�,� là trung điểm BC,CK��,��
→KE,BN,CP→��,��,�� đồng quy tại trọng tâm ΔKBCΔ���
Đúng 0
Bình luận (0)
1. cho tam giác ABC. trên nửa mặt phẳng chứa đỉnh C có bờ là đường thẳng AB ta dựng đoạn thẳng AE vuông góc với AB và AE AB. trên nửa mặt phẳng chứa đỉnh B có bờ là đường thẳng AC ta dựng đoạn thẳng AF vuông góc với AC và AF AC. đường thẳng EF cắt đường cao AD của tam giác ABC ở M. vẽ AH vuông góc EF cắt BC ở K ( H thuộc EF )a) tam giác ACK tam giác FAM b) M là trung điểm EFc) FB vuông góc với EC và FB EC2. cho tam giác ABC vuông tại A. AH là đường cao. đường phân giác góc B. góc C cắt nhau...
Đọc tiếp
1. cho tam giác ABC. trên nửa mặt phẳng chứa đỉnh C có bờ là đường thẳng AB ta dựng đoạn thẳng AE vuông góc với AB và AE = AB. trên nửa mặt phẳng chứa đỉnh B có bờ là đường thẳng AC ta dựng đoạn thẳng AF vuông góc với AC và AF = AC. đường thẳng EF cắt đường cao AD của tam giác ABC ở M. vẽ AH vuông góc EF cắt BC ở K ( H thuộc EF )
a) tam giác ACK = tam giác FAM
b) M là trung điểm EF
c) FB vuông góc với EC và FB = EC
2. cho tam giác ABC vuông tại A. AH là đường cao. đường phân giác góc B. góc C cắt nhau tại I ; đường phân giác góc B và BAH cắt nhau tại M ; đường phân giác góc C và góc CAH cắt nhau tại N. đường thẳng MN cắt AB,AC theo thứ tự tại B' và C'
a) CM I là trực tâm tam giác AMN
b) có kết luận gì về tam giác AB'C'
a) Xét tam giác ACK và tam giác FAM có :
AC = FA
\(\widehat{CAK}=\widehat{AFM}\) (Cùng phụ với góc \(\widehat{FAK}\) )
\(\widehat{ACK}=\widehat{FAM}\) (Cùng phụ với góc \(\widehat{DAC}\) )
\(\Rightarrow\Delta ACK=\Delta FAM\left(g-c-g\right)\)
b) Do \(\Delta ACK=\Delta FAM\left(cma\right)\Rightarrow FM=AK\)
Chứng minh hoàn toàn tương tự câu a ta có: \(\Delta ABK=\Delta EAM\left(g-c-g\right)\)
\(\Rightarrow ME=AK\)
Từ đó suy ra FM = ME hay M là trung điểm EF.
c) Kéo dài FB cắt EC tại J. Ta chứng minh \(\widehat{FJE}=90^o\)
Xét tam giác FAB và tam giác CAE có:
FA = CA
AB = AE
\(\widehat{FAB}=\widehat{CAE}\) (Cùng phụ với góc \(\widehat{BAC}\) )
\(\Rightarrow\Delta FAB=\Delta CAE\left(c-g-c\right)\)
\(\Rightarrow FB=CE\) và \(\widehat{AFB}=\widehat{ACE}\)
Xét tứ giác AFJE có:
\(\widehat{AFJ}+\widehat{FJE}+\widehat{JEA}+\widehat{EAF}=360^o\)
\(\Rightarrow\widehat{ACE}+\widehat{FJE}+\widehat{CEA}+\widehat{EAC}+90^o=360^o\)
\(\Rightarrow\widehat{FJE}+\widehat{ACE}+\widehat{CEA}+\widehat{EAC}=270^o\)
\(\Rightarrow\widehat{FJE}+180^o=270^o\)
\(\Rightarrow\widehat{FJE}=90^o\)
Vậy nên \(FB\perp EC\) (đpcm).
Đúng 0
Bình luận (0)
Bài 2:
a) Gọi giao điểm của đường phân giác ^ABC và ^ACB với AC và AB lần lượt là E và D
Dễ thấy: ^BAH=^ACB (Cùng phụ với ^HAC) => 1/2. ^BAH = 1/2. ^ACB
=> ^DAM=^ACD. Mà ^DAM+^MAC=^BAC=900 => ^ACD+^MAC=900 => AM \(\perp\)CD
hay NI\(\perp\)AM.
Tương tự ta chứng minh MI\(\perp\)AN
Xét tam giác MAN: NI\(\perp\)AM; MI\(\perp\)AN => I là trực tâm của tam giác MAN (đpcm).
b) Do I là trực tâm của tam giác AMN (cmt) => AI\(\perp\)MN hay AI\(\perp\)B'C'
Ta có: Tam giác ABC có 2 đường phân giác ^ABC và ^ACB cắt nhau tại I => AI là phân giác ^BAC
=> AI là phân giác ^B'AC'.
Xét tam giác AB'C': AI là phân giác ^B'AC'. Mà AI\(\perp\)B'C' => Tam giác AB'C' cân tại A
Lại có: ^B'AC'=900 => Tam giác B'AC' vuông cân tại A.
Đúng 0
Bình luận (0)
Câu hỏi của SKT_NTT - Toán lớp 7 - Học toán với OnlineMath bài này câu c làm thế nào nhỉ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.Câu 2: Cho hình thang cân ABCD, đáy lớn CD10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.Câu 4: Cho tam giác ABC vuông tại A, ABAC; gọi I là giao điểm các đường phân giác, M là...
Đọc tiếp
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.
Câu 2: Cho hình thang cân ABCD, đáy lớn CD=10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.
Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.
Câu 4: Cho tam giác ABC vuông tại A, AB<AC; gọi I là giao điểm các đường phân giác, M là trung điểm BC . Cho biết góc BIM bằng 90°. Tính BC:AC:AB.
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
Đúng 1
Bình luận (0)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
Đúng 0
Bình luận (0)


















