Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp

A. GM = GN

B.  G M →   +   G N →   =   0 →

C.  G A →   +   G B →   +   G C →   +   G D →   =   0

D.  P G →   =   1 / 4 ( P A →   +   P B →   +   P C →   +   P D → ) , với P là điểm bất kì.

Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.

Bộ ba vecto đồng phẳng là:

A. A B → ,   B C → ,   A D →

B.  M P → ,   B C → ,   A D →

C.  A C → ,   M P → ,   B D →

D.  M P → ,   P Q → ,   C D →

Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho P A →   =   m P D → và Q B →   =   m Q C → , với m khác 1. Vecto M P → bằng:

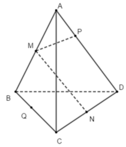
A.  M B → − m Q C →

B.  M N → − m P D →

C.  M A → − m P D →

D.  M N → − m Q C →