Trong
[
0
;
2
π
)
, phương trình sinx 1- cos2x có tập nghiệm là
Đọc tiếp
Trong [ 0 ; 2 π ) , phương trình sinx = 1- cos2x có tập nghiệm là
Những câu hỏi liên quan
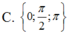
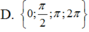
Số oxi hóa của Mn, Fe trong Fe3+, S trong SO3, P trong PO43- lần lượt là:
A. 0, +3, +6, +5.
B. 0, +3, +5, +6.
C. +3, + 5, 0, +6.
D. +5, +6, +3, 0.
Chọn đáp án đúng.
A đúng.
Mn là đơn chất nên có số oxi hóa 0
Fe3+ có số oxi hóa +3
SO3: x + 3.(-2) = 0 ⇒ x = 6 ⇒ số oxi hóa của S là +6
PO43-: x + 4.(-2) = -3 ⇒ x = 5 ⇒ số oxi hóa của P là +5
Đúng 0
Bình luận (0)
Trong quá trình chất khí nhận nhiệt và sinh công thì Q và A trong hệ thức δU = A + Q phải có giá trị nào sau đây?
A. Q < 0 và A > 0
B. Q > 0 và A > 0
C. Q > 0 và A < 0
D. Q < 0 và A < 0
- Chọn C.
- Vì vật nhận nhiệt thì Q > 0, vật sinh công thì A < 0.
Đúng 0
Bình luận (0)
Viết vào chỗ chấm (theo mẫu):a) Chữ số 0 trong số 30 522 cho biết chữ số hàng nghìn là 0.b) Chữ số 0 trong 8074 cho biết chữ số hàng .............. là ...............c) Chữ số 0 trong số 205 316 cho biết chữ số hàng ..............là ...............d) Chữ số 0 trong số 200 463 cho biết chữ số hàng ..............là .............. và chữ số .............. là ...............
Đọc tiếp
Viết vào chỗ chấm (theo mẫu):
a) Chữ số 0 trong số 30 522 cho biết chữ số hàng nghìn là 0.
b) Chữ số 0 trong 8074 cho biết chữ số hàng .............. là ...............
c) Chữ số 0 trong số 205 316 cho biết chữ số hàng ..............là ...............
d) Chữ số 0 trong số 200 463 cho biết chữ số hàng ..............là .............. và chữ số .............. là ...............
a) Chữ số 0 trong số 30 522 cho biết chữ số hàng nghìn là 0.
b) Chữ số 0 trong 8074 cho biết chữ số hàng trăm là 0.
c) Chữ số 0 trong số 205 316 cho biết chữ số hàng chục nghìn là 0.
d) Chữ số 0 trong số 200 463 cho biết chữ số hàng chục nghìn là 0 và chữ số hàng nghìn là 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc - 2ac abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là: A. 14 B.
14
C. 1/
14
D. Không tồn tại
Đọc tiếp
Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc - 2ac = abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là:
A. 14
B. 14
C. 1/ 14
D. Không tồn tại
Trong dãy 1, 0, 1, 0, 1, 0, 3, 5, 0 , … bắt đầu từ chữ số thứ bảy bằng chữ số hàng đơn vị của tổng sáu chữ số đứng trước nó. Hỏi trong dãy có xuất hiện lại 6 số 0, 1, 0, 1, 0, 1 không ?
Bài 7 : a) Tìm 5 danh từ biết trong mỗi từ đều có tiếng “sông”. Đặt câu với 1 trong các từ vừa tìm được........................................................................................................................................................................................................................................................................................................................b) Tìm 5 danh từ biết trong mỗi từ đều có tiếng “mưa”. Đặt câu với 1 trong các từ vừa...
Đọc tiếp
Bài 7 : a) Tìm 5 danh từ biết trong mỗi từ đều có tiếng “sông”. Đặt câu với 1 trong các từ vừa tìm được
........................................................................................................................................................................................................................................................................................................................
b) Tìm 5 danh từ biết trong mỗi từ đều có tiếng “mưa”. Đặt câu với 1 trong các từ vừa tìm được
........................................................................................................................................................................................................................................................................................................................
a. dòng sông, cửa sông, khúc sông, nước sông, sông cái .
Sông Hồng là một con sông cáib.cơn mưa, trận mưa, nước mưa, mưa rào, mưa xuân
Trời đang nắng bỗng nhiên một cơn mưa xuất hiện.
a) Sông băng
Sông núi
Dòng sông
Con sông
Sông Hồng
Dòng sông quanh co uốn lượn như dải lụa.
b) Mưa rào
Mưa ngâu
Mưa xuân
Mưa phùn
Cơn mưa
Mưa ngâu trắng xóa một vùng trời.
@Cỏ
#Forever
Xem thêm câu trả lời
Một người đi bộ trong 5 phút được 350m. Hỏi trong 8 phút người đó đi được bao nhiêu mét (quãng đường đi được trong mỗi phút đều như nhau)?
Tóm tắt:
5 phút : 350 m
8 phút : ... m?
Bài giải:
1 phút người đó đi được số mét là:
350 : 5 = 70 (m)
8 phút người đó đi được số mét là:
70 x 8 = 560 (m)
Đ/S : 560 m
Chắc thế đó! Chúc một ngày tốt lành!
Trong các nghiệm của phương trình cos 2 3 x cos 2 x - cos 2 x = 0 trong khoảng (0;π) là:
A. π/2
B. 3π/2
C. π
D. 2π
Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0), A’(6; 0; 0), B(0; 3; 0), B’(0 ;4; 0), C(0; 0; 4), C’(0; 0; 3).
Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
Đúng 1
Bình luận (0)
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.
Đúng 1
Bình luận (0)
Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0). Tính thể tích tứ diện SAB'C'
