Tìm giá trị của m để: Hai đường thẳng ( d 1 ): mx + 3y = 10; ( d 2 ): x – 2y = 4 cắt nhau tại một điểm trên trục Ox. Vẽ hai đường thẳng này trên cùng một mặt phẳng tọa độ.

Những câu hỏi liên quan
Cho hai đường thẳng
d
1
:
2
x
+
3
y
+
1
0
,
d
2
:
m
x
+
2
m
−
2
y
−
m
+
6
0
. Giá trị của m để hai đường thẳng song song là A.m 0 B.m - 4 C.m 4...
Đọc tiếp
Cho hai đường thẳng d 1 : 2 x + 3 y + 1 = 0 , d 2 : m x + 2 m − 2 y − m + 6 = 0 . Giá trị của m để hai đường thẳng song song là
A.m =0
B.m = - 4
C.m = 4
D.không tồn tại m thỏa mãn
Để hai đường thẳng song song thì:
m 2 = 2 m − 2 3 ≠ − m + 6 1 ⇔ m 2 = 2 m − 2 3 m 2 ≠ − m + 6 1 ⇔ 3 m = 4 m − 4 m ≠ − 2 m + 12 ⇔ m = 4 m ≠ 4
không tồn tại m thỏa mãn yêu cầu bài toán.
ĐÁP ÁN D
Đúng 0
Bình luận (0)
Cho điểm A(-2; 1) và hai đường thẳng d1: 3x – 4y + 2 0 và d2: mx + 3y – 3 0. Giá trị của m để khoảng cách từ A đến hai đường thẳng bằng nhau là: A.
m
±
1
B. m 1 và m 4 C.
m
±
4
D. m - 1 và m 4
Đọc tiếp
Cho điểm A(-2; 1) và hai đường thẳng d1: 3x – 4y + 2 = 0 và d2: mx + 3y – 3 = 0. Giá trị của m để khoảng cách từ A đến hai đường thẳng bằng nhau là:
A. m = ± 1
B. m = 1 và m = 4
C. m = ± 4
D. m =- 1 và m = 4
Sử dụng công thức khoảng cách ta có
3. − 2 − 4.1 + 2 3 2 + − 4 2 = m − 2 + 3.1 − 3 m 2 + 3 2
⇔ 8 5 = − 2 m m 2 + 9 ⇔ 8 m 2 + 9 = 10 m ⇔ 64 ( m 2 + 9 ) = 100 m 2 ⇔ 64 m 2 + 576 = 100 m 2 ⇔ 36 m 2 = 576 ⇔ m 2 = 16 ⇔ m = ± 4
Đáp án là phương án C.
Chú ý. Học sinh có thể thử lại các phương án được đưa ra để chọn đáp án đúng, tuy nhiên sẽ tốn nhiều thời gian hơn là làm bài toán trực tiếp.
Đúng 0
Bình luận (0)
Cho điểm A(-2; 1) và hai đường thẳng d1: 3x - 4y + 5 0 và d2: mx + 3y - 3 0. Giá trị của m để khoảng cách từ A đến d1 gấp hai lần khoảng cách từ A đến đường thẳng d2 là: A.
m
±
1
B.
m
±
15
3
C.
m
±
4
D.
m
...
Đọc tiếp
Cho điểm A(-2; 1) và hai đường thẳng d1: 3x - 4y + 5 = 0 và d2: mx + 3y - 3 = 0. Giá trị của m để khoảng cách từ A đến d1 gấp hai lần khoảng cách từ A đến đường thẳng d2 là:
A. m = ± 1
B. m = ± 15 3
C. m = ± 4
D. m = ± 15 5
Trong mặt phẳng Oxy, cho hai đường thẳng y=mx+3m+2 và (d1) y=x+1. Tìm giá trị của m để đường thẳng (d) và (d1) song song với nhau
Để hai đường thẳng song song mà không trùng nhau thì điều kiện cần và đủ là :
\(\hept{\begin{cases}m=1\\3m+2\ne1\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\m\ne-\frac{1}{3}\end{cases}\Leftrightarrow}m=1}\)
Tìm giá trị của m để hai đường thẳng y = mx + 1 và y = (m - 4)x - 2 cắt nhau
A. m ≠ 1
B. m ≠ 0
C. Với mọi m
D. Không tồn tại m
Đáp án C
Để hai đường thẳng đã cho cắt nhau thì m ≠ m - 4 ⇔ 0 ≠ -4
Vậy với mọi m thì hai đường thẳng luôn cắt nhau
Đúng 0
Bình luận (0)
Tìm giá trị của m để hai đường thẳng (d1): mx + y =1 và (d2): x - my = m + 6 cắt nhau tại một điểm M thuộc đường thẳng (d): x +2y = 8
MÌNH CẦN GẤP. MAI MÌNH THI RỒI
Tìm giá trị thực của m để hai đường thẳng d: y = mx − 3 và △ : y + x = m cắt nhau tại một điểm nằm trên trục tung.
A. m = -3
B. m = 3
C. m = ± 3
D. m = 0
Tìm giá trị của m để đường thẳng (d): y = (2m – 5)x – 5m đi qua giao điểm của hai đường thẳng ( d 1 ): 2x + 3y = 7 và ( d 2 ): 3x + 2y = 13
Gọi I là giao điểm của (
d
1
) và (
d
2
). Khi đó tọa độ của I là nghiệm của hệ phương trình: 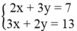
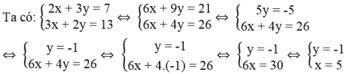
Tọa độ điểm I là I(5; -1)
Đường thẳng (d): y = (2m – 5)x – 5m đi qua I(5; -1) nên tọa độ của I nghiệm đúng phương trình đường thẳng:
Ta có: -1 = (2m – 5).5 – 5m ⇔ -1 = 10m – 25 – 5m
⇔ 5m = 24 ⇔ m = 24/5
Vậy với m = 24/5 thì đường thẳng (d) đi qua giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).
Đúng 1
Bình luận (0)
tìm giá trị của m để hai đường thẳng d1:mx+y=1 và d2:x-my=m+6 cắt nhau tại điểm M thuộc đường thẳng d:x+2y=8
Gọi A (x;y) là giao điểm của d, d1 và d2. tọa độ giao điểm điểm của A là nghiệm của hpt : d và d1. ( giải được nghiệm x, y sẽ chứa tham số m ), nếu có m ở mẫu thì tìm đk của xác định của m nhé
sau đó thay tọa độ A tìm được vào d2 sẽ tìm ra m .
Đúng 0
Bình luận (0)











