[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 3) ] 

|-----------------------------------------------------------------------------|

#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS 

(1) Phần số học: 

+ Các tính chất cơ bản giao hoán, kết hợp 

- Tính chất giao hoán được biểu hiện trong phép cộng và nhân 

CT: \(a+b+c=a+c+b\) 

       \(a\cdot b\cdot c=a\cdot c\cdot b\) 

Tính chất này khá quen ở cấp tiểu học và rất quan trọng ở cấp THCS 

- Tính chất kết hợp được biểu hiện ở trong phép cộng và nhân 

CT: \(a+b+c=\left(a+c\right)+b\)

      \(a\cdot b\cdot c=\left(a\cdot c\right)\cdot b\)

Tương tự giao hoán tính chất này rất quan trong để làm các dạng bài tập như:

VD: \(3,12+6+0,88=\left(3,12+0,88\right)+6=4+6=10\) 

+ Dấu hiệu chia hết cho các số từ 1 - 10 

- Tất cả các số chia hết cho 1 

- Chia hết cho 2:      

Các số chia hết cho 2 có các chữ số cuối cùng là 0, 2, 4, 6, 8 

VD: 12, 56, 96, ... 

- Chia hết cho 3: 

Dấu hiệu của một số chia hết cho 3 là tổng các chữ số đó sẽ chia hết cho 3:

CT: \(\overline{abcd}\) chia hết cho 3 khi \(a+b+c+d\) chia hết cho 3

VD: \(3210\) chia hết cho 3 vì \(3+2+1+0=6\) ⋮ 3 

- Chia hết cho 4:

Dấu hiệu của 1 số chia hết cho 4 khi 2 chữ số cuối cùng của số đó chia hết cho 4 đều này bắt buộc các bạn phải nhớ được các số chia hết cho 4 từ 0 - 99 

CT: \(\overline{abcd}\) chia hết cho 4 khi \(\overline{cd}\) chia hết cho 4 

VD: \(3456\) chia hết cho 4 khi 56 chia hết cho 4  

- Chia hết cho 5:

Dấu hiệu chia hết cho 5 là các số có chữ số cuối cùng là 5 hoặc 0

- Chia hết cho 6: 

Dấu hiệu của một số chia hết cho 6 là số đó vừa chia hết cho 2 vừa chia hết cho 3 

VD: 1230 chia hết cho 6 vì 1230 vừa chia hết cho 2 vừa chia hết cho  3

- Chia hết cho 7: 

Dấu hiệu của 1 số chia hết cho 7 là lấy 5 nhân cho chữ số tận cùng rồi cộng cho phần còn lại của số đó nếu chia hết cho 7 thì số đó chia hết cho 7 

CT: \(\overline{abcd}\)chia hết cho 7 khi \(5\cdot d+\overline{abc}\) ⋮ 7

VD: 182 chia hết cho 7 vì \(5\cdot2+18=28\) ⋮ 7 

- Chia hết cho 8 

Dấu hiệu 1 số chia hết cho 8 khi 3 chữ số cuối của số đó chia hết cho 8

VD: 1264 chia hết cho 8 khi 3 chữ số cuối của nó chia hết cho 8 

- Chia hết cho 9

Dấu hiệu của 1 số chia hết cho 9 khi tổng các chữ số của số đó tạo thành 1 số chia hết cho 4

CT: \(\overline{abcd}\) chia hết cho 8 khi \(a+b+c+d\) ⋮ 9

VD: 36 chia hết cho 9 vì 3 + 6 chia hết cho 9 

- Chia hết cho 10 

Dấu hiệu chia hết cho 10 là chữ số tận cùng của số đó là số 0 

VD: 120 chia hết cho 10 vì có chữ số tận cùng là số 0 

+ Quy tắc dấu của các phép cộng trừ nhân chia các số nguyên 

- Phép cộng: 

\(a+b=a+b\)

\(\left(-a\right)+\left(-b\right)=-\left(a+b\right)\)

\(a+\left(-b\right)=a-b\)

\(-a+b=b-a\)

- Phép trừ:

\(a-b=a-b\)

\(-a-b=-\left(a+b\right)\)

\(a-\left(-b\right)=a+b\)

- Phép nhân:

\(a\cdot b=a\cdot b\)

\(-a\cdot-b=a\cdot b\)

\(a\cdot-b=-\left(a\cdot b\right)\)

\(-a\cdot b=-\left(a\cdot b\right)\)

- Phép chia:

\(a:b=a:b\)

\(-a:-b=a:b\)

\(-a:b=-\left(a:b\right)\)

\(a:-b=-\left(a:b\right)\)

Lưu ý: Khi mở/ đóng ngoặc nếu trước dấu ngoặc đó là dấu + thì dữ nguyên nếu trước dấu ngoặc đó là dấu - thì đổi dấu tất cả hạng tử của phép tính đó:

VD: \(-\left(a-b-c\right)=-a+b+c\)

+ Tính chất dãy tỉ số bằng nhau 

Ta có tính chất này:

Nếu: \(\dfrac{a}{m}=\dfrac{b}{n}\) (với m,n là số nguyên ≠ biến) và biết \(a\pm b=?\) thì ta có thể tìm được a,b như sau:

VD: \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{a+b}{2+3}=\dfrac{5}{5}=1\) (biết \(a+b=5\)) 

\(\Rightarrow\left\{{}\begin{matrix}a=2\cdot1=2\\b=3\cdot1=3\end{matrix}\right.\)

Công thức tổng quát: \(\dfrac{a_1}{m_1}=\dfrac{a_2}{m_2}=\dfrac{a_3}{m_3}=...=\dfrac{a_n}{m_n}=\dfrac{a_1+a_2+...+a_n}{m_1+m_2+...+m_n}\)

(2) Phần hình học 

+ Các trường hợp bằng nhau của tam giác 

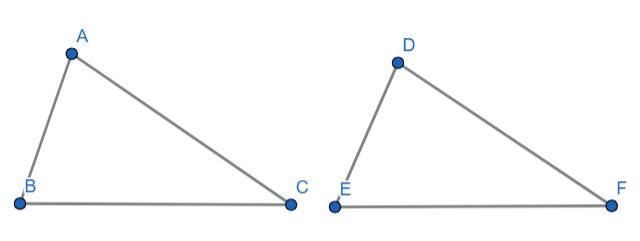
- Trường hợp 1:

Nếu 3 cạnh của tam giác này bằng 3 cạnh của tam giác kia thì 2 tam giác này bằng nhau

Xét ΔABC và ΔDEF ta có:

\(AB=DE\left(gt\right)\)

\(AC=DF\left(gt\right)\)

\(BC=EF\left(gt\right)\)

\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(c.c.c\right)\) 

- Trường hợp 2: 

Nếu 2 cạnh của tam giác này bằng 2 cạnh của tam giác kia và 1 góc nằm giữa 2 cạnh này của tam giác này bằng góc nằm giữa 2 cạnh này của tam giác kia thì hai tam giác bằng nhau 

Xét ΔABC và ΔDEF ta có: 

\(AB=DE\left(gt\right)\) 

\(AC=DF\left(gt\right)\)

\(\widehat{A}=\widehat{D}\left(gt\right)\)

\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(c.g.c\right)\)

- Trường hợp 3: 

Nếu 1 cạnh của tam giác này bằng 1 cạnh của tam giác kia và 2 góc kề cạnh này của tam giác này bằng 2 góc kề cạnh này của tam giác kia thì hai tam giác bằng nhau

Xét ΔABC và ΔDEF ta có:

\(\widehat{A}=\widehat{D}\left(gt\right)\)

\(AB=DE\left(gt\right)\)

\(\widehat{B}=\widehat{E}\left(gt\right)\)

\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(g.c.g\right)\)

+ Định lý Py-ta-go thuận và đảo

- Theo định lý Py-ta-go thì trong 1 tam giác vuông thì tổng bình phương của hai cạnh góc vuông bằng bình phương của cạnh huyền (nhận biết cạnh huyền: cạnh đối diện với góc vuông thì cạnh đó là cạnh huyền

Theo ĐL Py-ta-go trong tam giác vuông: \(a^2+b^2=c^2\) (1) (a,b là cạnh góc vuông, c là cạnh huyền) 

Từ công thức thên ta có thể tính được toàn bộ các cạnh của tam giác vuông khi biết 2 cạnh còn lại 

Từ (1) \(\Rightarrow\left\{{}\begin{matrix}c=\sqrt{a^2+b^2}\\a=\sqrt{c^2-b^2}\\b=\sqrt{c^2-a^2}\end{matrix}\right.\) 

- Định lý Py-ta-go đảo được dựa trên định lý Py-ta-go thuận nên nếu trong 1 tam giác bình phương của cạnh này bằng tổng bình phương của 2 cạnh còn lại thì tam giác đó là tam giác vuông (góc đối diện với cạnh bằng tổng bình phương hai cạnh kia chính là góc vuông) 

Theo định lý Py-ta-go đảo: \(c^2=a^2+b^2\Rightarrow\text{Δ}\) đó vuông     

VD: Cho tam giác ABC vuông tại A và AB=3(cm), AC=4(cm). Tính BC

Xét ΔABC vuông tại A áp dụng định lý Py-ta-go ta có:

\(BC^2=AC^2+AB^2\)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)

\(\Rightarrow BC=\sqrt{3^2+4^2}=\sqrt{25}=5\left(cm\right)\) 

+ Bộ 3 độ dài cạnh của tam giác

Để xác định được bộ 3 độ dài cạnh của tam giác thì ta có nhận xét sau: 

\(\left\{{}\begin{matrix}a+b>c\\a+c>b\\b+c>a\end{matrix}\right.\Rightarrow a,b,c\) là bộ 3 độ dài cạnh của tam giác 

VD: cho tam giác ABC có: AB = 1(cm), AC=1,5(cm), BC=5(cm) 

Ta có:

\(\left\{{}\begin{matrix}AB+AC< BC\left(1+1,5< 5\right)\\BC+AB>AC\left(1+5>15\right)\\BC+AC>AB\left(5+1,5>1\right)\end{matrix}\right.\)

Vậy bộ 3 độ dài của của tam giác ABC là không đúng 

________________________________________

*Cách học môn toán không bị nhàm chán và thú vi cần biết các tips sau: *  

- Không được học liên tiếp 2 - 3 giờ sẽ khiến cho cơ thể mệt mỏi buồn ngủ không hiệu quả

- Để không bị mất gốc thì nên học toàn chú trọng vào các ý chính (VD: ghi nhớ, các điều mà thầy cô lưu ý học) 

- Không cần thuộc lòng quan trọng là biết vận dụng vào bài toán 

- Cần lưu ý các kiến thức toán cở cấp độ của mình (tiểu học, THCS, THPT) 

- Phối hợp việc học toán và việc giải trí tránh bị nhàm chán mất tinh thần

- Sử dụng sơ đồ tư duy, takennotes, ...

- Lại đi làm lại nhiều lần dạng bài còn yếu

- Ôn lại nhiều lần các kiến thức, khái niệm, công thức... 

- Sử dụng nhiều kĩ thuật nhớ lâu, nhanh 

Các bạn hay anh chị có các tips học toán thú vị hơn mong anh chị bình luận ở đây nhé (trân trọng) 

(* Nếu trong part 3 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *)  

[GỬI LỜI CHÚC THẬT Ý NGHĨA ĐẾN TẤT CẢ CÁC THÀNH VIÊN HOC24 - OLM]

--------------------------------------- 

Hôm nay cũng đã là ngày 10 rồi từ ngày khai giảng ở tất cả các trường trên khắp cả nước đến nay đã 5 ngày hầu như các thành viên trong HOC24 - OLM đã được đi học trong tuần đầu tiền này, có thể các bạn sẽ được gặp lại bạn cũ của mình ở các năm trước. Riêng mình đó chỉ còn là những kỉ niệm đẹp mà thôi vi năm trước mình học là 8A10 do 1 số lý do của nhà trường mà lớp mình phải bị chia 

Các bạn tạm biệt mùa hè đáng nhớ này và bước vào năm học mới và lớn hơn 1 tuổi mình nghĩ dù là ai thì cũng trưởng thành hơn rất nhiều và thực sự các bạn 2k9 bằng tuổi mình và các anh chị 2k6 phải vất vả hơn nhiều vì phải ôn thi chuyển cấp và thi tốp nghiệp, ai cũng có 1 ước mơ dành cho riêng mình vì vậy các bạn phải phấn đấu vì ước mơ đó. 

" Hãy gửi lời chúc của mình đối với tất cả các thành viên của HOC24 và nêu lên kỉ niệm đầu năm của cho các bạn khác nghe nhé ! "  

===============================

Nhiệm kì 21 (nhiệm kì hè) của các CTV / CTVVIP HOC24, OLM đã gần kết thúc và trước khi bước qua nhiệm kì 22 (nhiệm kì HKI) thì mình xin gửi lời chúc và lời cảm ơn trân thành đến với các CTV / CTVVIP ở nhiệm kì này cảm ơn rất nhiều đã giúp đỡ và đưa CĐ HOC24 đi lên theo chiều hướng tích cực 

+ Các CTV hoạt động tích chăm chỉ ở môn toán

 MinYewCou 

 Thư Thư 

 Ngô Hải Nam 

 Kurouba Ryousuke 

 Kumuro Tairoku 

 Hquynh 

 Kiều Vũ Linh 

 Dora 

+ Các CTV hoạt động tích chăm chỉ ở môn tiếng anh 

 Anh Thư Bùi

 Ngô Bá Hùng

 Đăng khoa

 Khinh Yên 

 (.I_CAN_FLY.)

 _Sunn So Sad_  

+ Các CTV hoạt động tích chăm chỉ ở môn khoa học tự nhiên 

 huehan huynh 

 Kudo Shinichi 

 ひまわり 

 Phước Lộc

 TV Cuber

 Khánh Đan 

 Đào Tùng Dương 

+ Các CTV hoạt động tích chăm chỉ ở môn ngữ văn 

 Đỗ Tuệ Lâm 

 Đoàn Trần Quỳnh Hương 

+ Các CTVVIP cực kì tích cực và chăm chỉ trong nhiệm kì này

 POP POP

 Nguyễn Quốc Đạt 

 Đỗ Thanh Hải

 Lê Nhật Ninh 

 Minh Nguyệt 

 Minh Lệ 

+ Em cảm ơn rất nhiều các Thầy/Cô đã giúp đỡ các em trong HOC24 và OLM ạ 

Thầy Hà Đức Thọ 

Cô Tuyết Ngọc

Cô Ngô Phương 

Quoc Tran Anh Le

Hà Quang Minh   

- Và em xin chúc kì CTV 22 này diễn ra thành công và có nhiều bạn/ anh/ chị mới được thêm vào đội ngũ CTV này ạ, em sẽ trở thành 1 CTV và không mắc sai lầm nhưng trước nữa ạ mong các anh chị / thầy cô giúp đỡ ạ 

[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 2) ] 

|-----------------------------------------------------------------------------|

#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS

(1) Phần số học 

+ Số nguyên tố, phân tích một số ra thừa số nguyên tố 

- Ở cấp THCS ta cần nắm và hiểu rõ về số nguyên tố 

Số nguyên tố là số tự nhiên khác 1 và chia hết cho 1 và chia hết cho chính nó 

VD: \(3,5,7,11,13,17,19,23,29,...\) 

- Cách phân tích 1 số ra thừa số nguyên tố 

Bước 1: Nhìn sơ quát số và nhẩm xem số đó chia hết cho 2,3,5 hay 7 không 

Bước 2: Xét thương nếu thương không phải số nguyên tố thì tiếp tục phân tích 

Bước 3: Tiếp tục phân tích thương dần đến kết quả cuối cùng là 1 số nguyên tố 

VD: Phân tích số 35 

Ta có: 35 = 7 x 5 

+ Ước, bội, ước chung lớn nhất, bội chung nhỏ nhất

- Tập hợp các số mà số đó chia hết được gọi là ước 

Được kí hiệu là Ư(x) 

- Tập hợp các số chia hết cho số đó được gọi là bội 

Được kí hiệu là B(x) 

VD: Ư(10)\(=\left\{1;2;5;10\right\}\) 

       \(B\left(10\right)=\left\{0;10;20;30;40;50;...\right\}\) 

- Ước chung là tập hợp ước của số này mà cũng là ước của số kia 

Được kí hiệu là: ƯC(x;y) 

- Bội chung là tập hợp bội của số này mà cũng là bội của số kia 

Được kí hiệu là BC(x;y) 

VD: \(Ư\left(12\right)=\left\{1;2;3;4;6;12\right\}\)

       \(Ư\left(15\right)=\left\{1;3;5;15\right\}\)

\(\RightarrowƯC\left(12;15\right)=\left\{1;3\right\}\)

       \(B\left(9\right)=\left\{0;9;18;27;36;54;...\right\}\)

       \(B\left(3\right)=\left\{0;3;6;9;12;15;18;21;24;27;...\right\}\)

\(\Rightarrow BC\left(9;3\right)=\left\{0;9;18;27;..\right\}\)

- Ước chung lớn nhất là ước của số này cũng là ước của số kia nhưng đó là ước chung lớn nhất 

Được kí hiệu là: ƯCLN

- Bội nhung nhỏ nhất là bội của số này cũng là bội của số kia nhưng đó là bội chung nhỏ nhất 

Được kí hiệu là: BCNN 

+ Số hữu tỉ, vô tỉ, số thập phân hữu hạn, vô hạng tuần hoàn, giá trị tuyệt đối

- Số hữu tỉ được biểu diễn dưới dạng \(\dfrac{a}{b}\left(a,b\in Z;b\ne0\right)\) 

Tập hợp các số hữu tỉ được kí hiệu là tập hợp Q 

- Số thập phân hữu hạn là số hữu tỉ tối giản không có ước nguyên tố khác 2 và 5 

VD: \(\dfrac{1}{5};\dfrac{2}{5};\dfrac{5}{2};...\)

- Số thập phân vô hạn tuần hoàn là số hữu tỉ có ước nguyên tố khác 2,5 

VD: \(\dfrac{3}{7};\dfrac{1}{6};\dfrac{1}{9};\dfrac{5}{7};...\)

- Cách công trừ nhân chia các số hữu tỉ:

Cộng số hữu tỉ:

\(\dfrac{a}{m}+\dfrac{b}{m}=\dfrac{a+b}{m}\)

Trừ số hữu tỉ:

\(\dfrac{a}{m}-\dfrac{b}{m}=\dfrac{a-b}{m}\)

Nhân số hữu tỉ:

\(\dfrac{a}{n}\cdot\dfrac{b}{m}=\dfrac{a\cdot b}{m\cdot n}\)

Chia số hũu tỉ:

\(\dfrac{a}{n}:\dfrac{b}{m}=\dfrac{a}{n}\cdot\dfrac{m}{b}=\dfrac{a\cdot m}{n\cdot b}\)

- Tính giá trị tuyệt đối của 1 số hữu tỉ: 

\(\left\{{}\begin{matrix}khi:x\ge0\Rightarrow\left|x\right|=x\\khi:x< 0\Rightarrow\left|x\right|=-x\end{matrix}\right.\)

VD: \(\left|-5\right|=-\left(-5\right)=5\left(-5< 0\right)\) 

       \(\left|2\right|=2\left(2>0\right)\)

(2) Phần hình học 

+ Một đường thẳng cắt 2 đường thẳng song song, hai góc so le trong, đồng vị, trong cùng phía

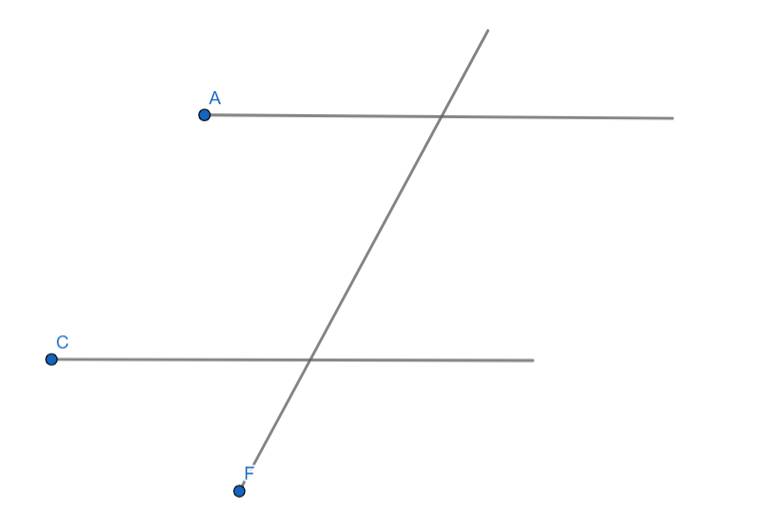
Lúc này ta có: \(A//C\) và \(F\) cắt \(A,C\)

Khi 1 đường thẳng cắt 2 đường thẳng song song sẽ tạp ra các cặp góc: so le trong, đồng vị, trong cùng phía 

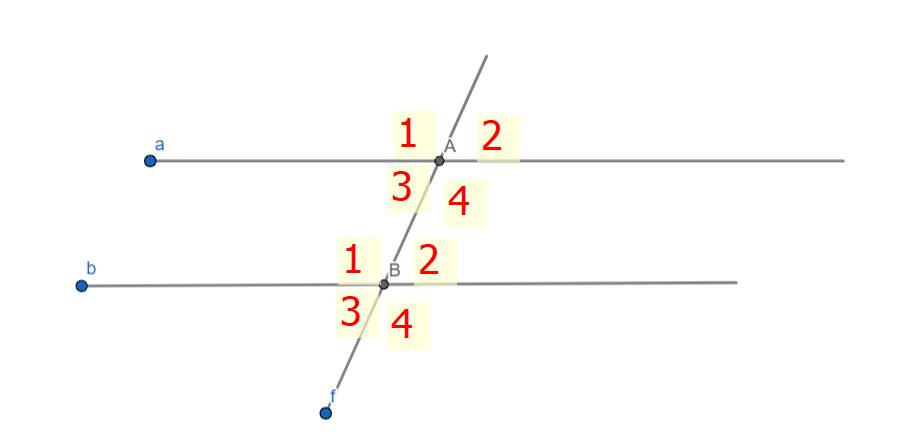
Khai niệm:

Hai góc đồng vị là 2 góc có cùng vị trí trong hai đường thẳng song song bị cắt bởi 1 đường thẳng 

- Hai góc đồng vị có cùng số đo với nhau 

VD: hai góc đồng vị trong hình: 

\(\left(\widehat{A_1};\widehat{B_1}\right);\left(\widehat{A_2};\widehat{B_2}\right);\left(\widehat{A_3};\widehat{B_3}\right);\left(\widehat{A_4};\widehat{B_4}\right)\)

Hai góc so le trong là so le với nhau trong hai đường thẳng song song bị cắt bởi 1 đường thẳng 

- Hai góc so le trong có cùng số đo với nhau  

VD: hai góc so le trong ở trong hình: \(\left(\widehat{A_3};\widehat{B_2}\right);\left(\widehat{A_4};\widehat{B_1}\right)\)

Hai góc trong cùng phía là hai góc này bên trong 2 đường thẳng và cùng 1 phía trong hai đường thẳng song song bị cắt bởi 1 đường thẳng  

- Hai góc trong cùng phía có tổng số đo là 180^o  

VD: hai góc trong cùng phía trong hình là: 

\(\left(\widehat{A_3};\widehat{B_1}\right);\left(\widehat{A};\widehat{B_2}\right)\)

+ Diện tích hình chữ nhật hình vuông, hình tam giác, hình thang; hình bình hành; hình thoi,....

Với: 

\(a\): cạnh đáy (chiều dài) 

\(b\) :cạnh đáy lớn (chiều rộng) 

\(h\): là chiều cao 

\(d\): là đường chéo 

- Diện tích hình chữ nhật:

\(S=a\times b\)

- Diện tích hình vuông:

\(S=a\times a=a^2\)

- Diện tích hình tam giác:

\(S=\dfrac{1}{2}\times a\times h\)

- Diện tích hình thang:

\(S=\dfrac{a+b}{2}\times h\)

- Diện tích hình bình hành:

\(S=a\times h\)

- Diện tích hình thôi:

\(S=\dfrac{d_1\times d_2}{2}\)  

+ Diện tích xung quanh, diện tích toàn phần, thể tích hình hộp chữ nhật, hình lập phương 

Với:

\(a\): cạnh (chiều rộng) 

\(b\): chiều dài 

\(h\): chiều cao 

- Diện tích xung quanh của hình hộp chữ nhật:
\(S_{xq}=\left(a+b\right)\times2\times h\)

- Diện tích toàn phần của hình hộp chữ nhật:

\(S_{tp}=S_{xq}+S_đ\times2=\left(a+b\right)\times2\times h+a\times b\times2\)

- Thể tích hình hộp chữ nhật:

\(V=a\times b\times h\)

- Diện tích xung quanh hình lập phương: 

\(S_{xq}=\left(a+a\right)\times2\times a=4a^2\)

- Diện tích toàn phần của hình lập phương là: 

\(S_{tp}=S_{xq}+S_đ\times2=4a^2+2a^2=6a^2\)

- Thể tích hình lập phương là:

\(V=a\times a\times a=a^3\)

__________________________________________

*Cách học môn toán không bị nhàm chán và thú vi cần biết các tips sau: *  

- Không được học liên tiếp 2 - 3 giờ sẽ khiến cho cơ thể mệt mỏi buồn ngủ không hiệu quả

- Để không bị mất gốc thì nên học toàn chú trọng vào các ý chính (VD: ghi nhớ, các điều mà thầy cô lưu ý học) 

- Không cần thuộc lòng quan trọng là biết vận dụng vào bài toán 

- Cần lưu ý các kiến thức toán cở cấp độ của mình (tiểu học, THCS, THPT) 

- Phối hợp việc học toán và việc giải trí tránh bị nhàm chán mất tinh thần

- ....

Các bạn hay anh chị có các tips học toán thú vị hơn mong anh chị bình luận ở đây nhé (trân trọng) 

(* Nếu trong part 1 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *)     

[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part1) ] 

|-----------------------------------------------------------------------------|

#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS

(1) Phần số học: 

+ Tập hợp, số phần tử, cách chỉ ra tính chất đặc trưng, tổng dãy,... 

Trong toán học tập hợp gồm có các phần tử có đặt điểm chung nào đó, để kí hiệu 1 tập hợp ta dùng các chữ cái in hoa: A, B, C, D,... để gọi tên chung cho tập hợp đó như tập hợp A, B,... sau đó dùng dấu " = " và dấu { } để biểu diễn các phần tử của tập hợp trong đó để ngăn cách phẩn tử 1 với phần tử 2 ta dùng dấu " ; "

VD: Viết tập hợp A gồm các số tự nhiên nhỏ hơn 10 (1) 

\(A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)

Để chỉ ra tính chất đặt trưng của 1 tập hợp ta chú ý vào yêu cầu của tập hợp:

VD: Trong để (1) có tập hợp A gồm các số " tự nhiên " nên ta khẳng định \(x\in N^+\) (x là các phần tử của A 

Và là các số nhỏ hơn 10 nên: \(x< 10\) ta viết như sau: 

\(A=\left\{x\in N|x< 10\right\}\)

Để tính số phần tử của 1 tập hợp ta có công thức:

(phần tử lớn nhất - phần tử nhỏ nhất) :  số bước + 1 

+ Số bước là khoảng cách giữa hai phần tử: 1; 2; 3; ... ⇒ số bước là: 1 

Tính tổng của dãy số cách đều ta có công thức:

(phần tử lớn nhất + phần tử nhỏ nhất) x số phần tử : 2 

+ Lũy thừa, nhân; chia lũy thừa, ... 

Lũy thừa gồm có 2 phần: cơ số và số mũ

VD: \(2^3\) trong đó:

Cơ số: 2

Số mũ: 3 

Tính lũy thừa: \(2^3=2\cdot2\cdot2=8\) 

- Nhân, chia lũy thừa cùng cơ số: 

Ta có: \(a^m\) và \(a^n\) có cùng cơ số a

Để nhân hai lũy thừa này ta có công thức tổng quát như sau: 

\(a^m\cdot a^n=a^{m+n}\)

Tương tự khi chia hai lũy thừa này ta có công thức tổng quát:

\(a^m:a^n=a^{m-n}\)

- Nhân chia lũy thừa cùng số mũ: 

Ta có hai lũy thừa: \(m^a\) và \(n^a\) có cùng số mũ a 

Để nhân 2 lũy thừa này công thức tổng quát: 

\(m^a\cdot n^a=\left(m\cdot n\right)^a\)

Để chia 2 lũy thừa này ta có công thức tổng quát: 

\(m^a:n^a=\left(m:n\right)^a\)

Chú ý: nếu lũy thừa đó có số mũ chẵn thì lũy thừa đó luôn dương  

(2) Phần hình học 

+ Góc, góc nhọn, tù, vuông, bẹt,...

Góc là những gì nằm giữa hai đường thẳng cắt nhau tại 1 điểm:

VD: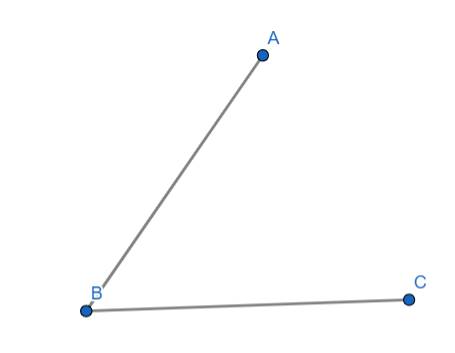 

Để kí hiệu tên của một góc có hai cách: 

C1: ∠ABC gọi tên góc ABC 

C2: \(\widehat{ABC}\) gọi tên góc ABC 

Có 4 loại góc: 

- Góc nhọn: là góc có số đo nhỏ hơn 90^o 

- Góc tù: là góc có số đo lớn hơn 90^o 

- Góc vuông: là góc có số đo bằng 90^o

- Góc bẹt: là góc có số đo bằng 180^o  

+ Hai góc kề, kề bù, phụ nhau, đối đỉnh,...  

- Hai góc kề nhau là hai góc có chung 1 cạnh và có hai cạnh kia ở hai mặt phẳng khác nhau có bờ là cạnh chung

VD: 

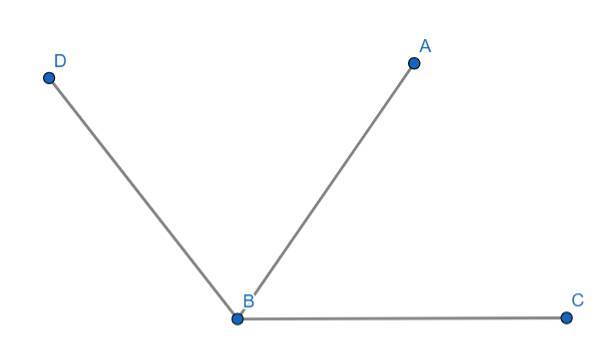
Trong đó: 

\(\widehat{ABC}\) và \(\widehat{\text{D}BA}\) kề nhau và tổng số đó của hai góc này sẽ bằng số đo của góc lớn mà chũng tạo thành 

\(\Rightarrow\widehat{ABC}+\widehat{DBA}=\widehat{DBC}\)

- Hai góc kề bù là hai góc có tổng số đo là 180^o hay tổng của hai góc đó sẽ tạo thành 1 góc bẹt 

VD: 

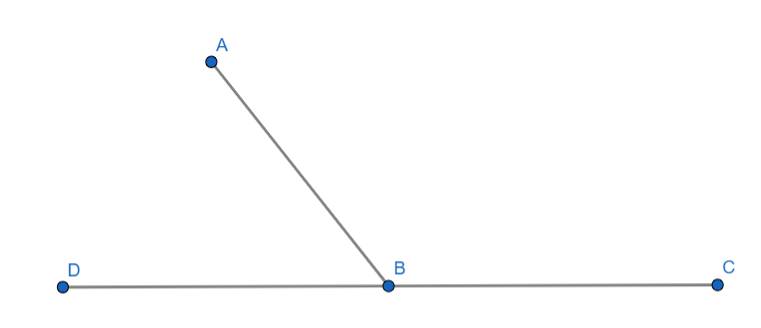
Trong đó: 

\(\widehat{DBA}\) và \(\widehat{ABC}\) là hai bù nhau tổng của hai góc là 180^o 

\(\Rightarrow\widehat{DBA}+\widehat{ABC}=180^o=\widehat{DBC}\) (Do hai góc đồng thời cũng là hai góc kề nhau) 

- Hai góc phụ nhau là hai góc có tổng số đo là: 90^o hay tổng số đo của hai góc đó sẽ tạo thành 1 góc vuông 

VD: 

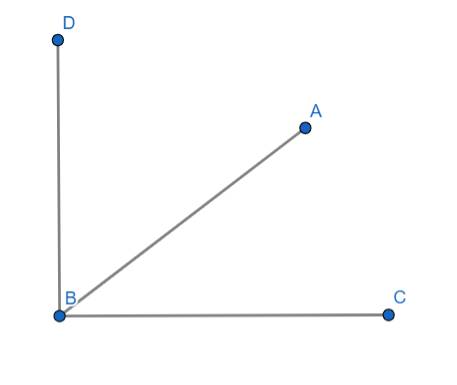
Trong đó:

\(\widehat{DBA}\) và \(\widehat{ABC}\) là hai góc phụ nhau 

\(\Rightarrow\widehat{DBA}+\widehat{ABC}=90^o=\widehat{DBC}\) (Do hai góc đồng thời cũng là hai góc kề nhau)  

- Hai góc đổi đỉnh là hai góc có số đo góc bằng nhau mà cạnh của góc này này là tia đối của góc kia 

VD: 

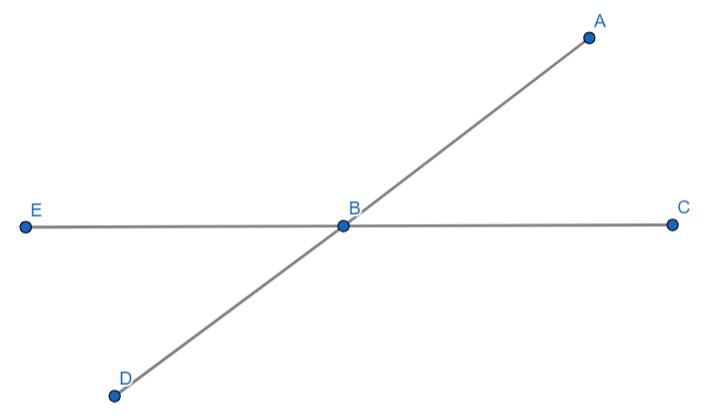
Khi đó: CE và AD cắt nhau tại B tạo ra các cặp góc đối đỉnh bằng nhau:

\(\widehat{EBD}=\widehat{ABC}\)

\(\widehat{EBA}=\widehat{DBC}\)

__________________________________________________________

(* Nếu trong part 1 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *) 

[THÔNG BÁO] Các khoá học lớp 4, lớp 8 và lớp 11 chính thức ra mắt trên OLM.VN từ ngày 15.6.2023!
👉 Nội dung bài giảng và các bài tập, đề kiểm tra bám sát các yêu cầu cần đạt mà Bộ Giáo dục và Đào tạo ban hành cho từng môn, lớp.
🎯 Phương pháp giảng dạy hiện đại, tích cực hoá các hoạt động học tập, tăng cường khả năng vận dụng kiến thức vào thực tiễn cho học sinh.
✅ Hệ thống bài giảng, bài tập trực quan, hấp dẫn, kết hợp sát thực tế, đáp ứng nhu cầu của mọi đối tượng học sinh.
✍ Đội ngũ giáo viên kinh nghiệm, tận tâm, sẵn sàng trao đổi các vướng mắc của học sinh trong mỗi bài giảng và đưa ra các định hướng hỗ trợ để các em tự học một cách hiệu quả nhất.
Thông tin chi tiết: https://olm.vn/bai-viet/olm-bo-sung-cac-khoa-hoc-theo-sgk-moi-lop-4-8-11-645403243
Tất cả các tài khoản VIP đều được tham dự các khóa học này.
Liên hệ với số điện thoại/Zalo sau để được tư vấn, hỗ trợ: 0898 987 672 (cô Hòa).
Trân trọng.